Trusted answers to developer questions
How to use bidirectional search implementation in Python
Ethel Esenam Klu
A graph is a network of nodes connected by arcs or edges.
The two basic graph search algorithms,
A graph search is done in one direction, either from the source/initial vertex to the goal/target vertex.
To search from both ends simultaneously, a bidirectional search is implemented.
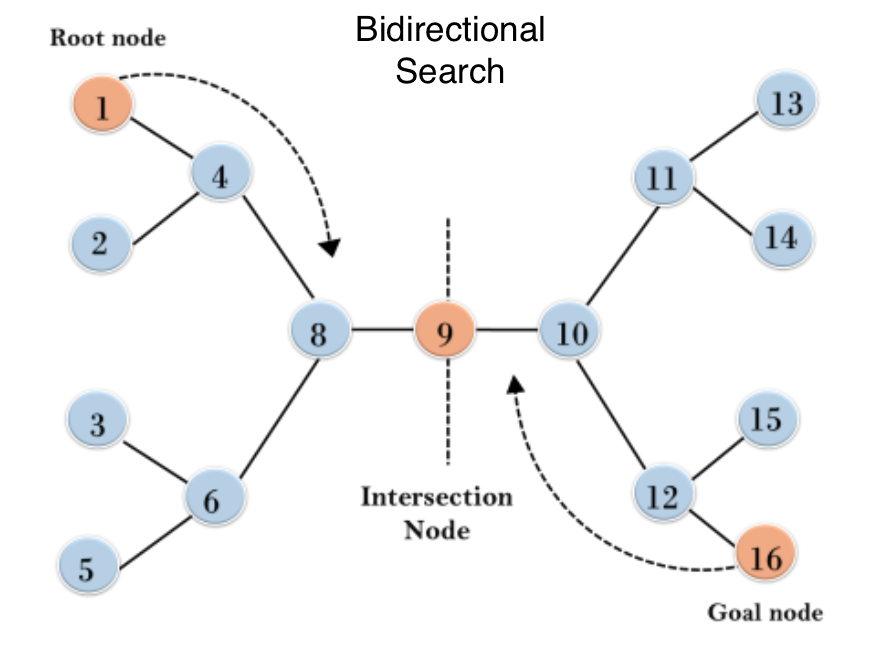
Bidirectional search
Bidirectional search is a graph search algorithm that finds the shortest path from a source vertex to a goal vertex.
In implementing bidirectional search in Python, the graph search can either be:
- Forward search from the source to the goal vertex.
- Backward search from the goal to the source vertex.
The intersection of both forward and backward graphs indicates the end of the search, as displayed below.
Advantages and disadvantages of bidirectional search in Python
| Advantage | Disadvantage |
|---|---|
| 1. Less time consuming as the shortest path length is used for the search. | The goal node has to be known before the search can be done simultaneously in both directions. |
When is it possible to use bidirectional search in Python?
The bidirectional approach can be used:
- When the branching factor for the forward and reverse direction is the same.
- When both the source and goal vertices are specified and distinct from each other.
Bidirectional search implementation in Python
Below is an implementation of bidirectional search in Python using BFS:
class adjacent_Node:
def __init__(self, v):
self.vertex = v
self.next = None
class bidirectional_Search:
def __init__(self, vertices):
self.vertices = vertices
self.graph = [None] * self.vertices
self.source_queue = list()
self.last_node_queue = list()
self.source_visited = [False] * self.vertices
self.last_node_visited = [False] * self.vertices
self.source_parent = [None] * self.vertices
self.last_node_parent = [None] * self.vertices
def AddEdge(self, source, last_node):
node = adjacent_Node(last_node)
node.next = self.graph[source]
self.graph[source] = node
node = adjacent_Node(source)
node.next = self.graph[last_node]
self.graph[last_node] = node
def breadth_fs(self, direction = 'forward'):
if direction == 'forward':
current = self.source_queue.pop(0)
connected_node = self.graph[current]
while connected_node:
vertex = connected_node.vertex
if not self.source_visited[vertex]:
self.source_queue.append(vertex)
self.source_visited[vertex] = True
self.source_parent[vertex] = current
connected_node = connected_node.next
else:
current = self.last_node_queue.pop(0)
connected_node = self.graph[current]
while connected_node:
vertex = connected_node.vertex
if not self.last_node_visited[vertex]:
self.last_node_queue.append(vertex)
self.last_node_visited[vertex] = True
self.last_node_parent[vertex] = current
connected_node = connected_node.next
def is_intersecting(self):
#
for i in range(self.vertices):
if (self.source_visited[i] and
self.last_node_visited[i]):
return i
return -1
def path_st(self, intersecting_node,
source, last_node):
path = list()
path.append(intersecting_node)
i = intersecting_node
while i != source:
path.append(self.source_parent[i])
i = self.source_parent[i]
path = path[::-1]
i = intersecting_node
while i != last_node:
path.append(self.last_node_parent[i])
i = self.last_node_parent[i]
print("*****Path*****")
path = list(map(str, path))
print(' '.join(path))
def bidirectional_search(self, source, last_node):
self.source_queue.append(source)
self.source_visited[source] = True
self.source_parent[source] = -1
self.last_node_queue.append(last_node)
self.last_node_visited[last_node] = True
self.last_node_parent[last_node] = -1
while self.source_queue and self.last_node_queue:
self.breadth_fs(direction = 'forward')
self.breadth_fs(direction = 'backward')
intersecting_node = self.is_intersecting()
if intersecting_node != -1:
print("Path exists between {} and {}".format(source, last_node))
print("Intersection at : {}".format(intersecting_node))
self.path_st(intersecting_node,
source, last_node)
exit(0)
return -1
if __name__ == '__main__':
n = 17
source = 1
last_node = 16
my_Graph = bidirectional_Search(n)
my_Graph.AddEdge(1, 4)
my_Graph.AddEdge(2, 4)
my_Graph.AddEdge(3, 6)
my_Graph.AddEdge(5, 6)
my_Graph.AddEdge(4, 8)
my_Graph.AddEdge(6, 8)
my_Graph.AddEdge(8, 9)
my_Graph.AddEdge(9, 10)
my_Graph.AddEdge(10, 11)
my_Graph.AddEdge(11, 13)
my_Graph.AddEdge(11, 14)
my_Graph.AddEdge(10, 12)
my_Graph.AddEdge(12, 15)
my_Graph.AddEdge(12, 16)
out = my_Graph.bidirectional_search(source, last_node)
if out == -1:
print("No path between {} and {}".format(source, last_node))
RELATED TAGS
python
twcompetition
communitycreator
CONTRIBUTOR
Ethel Esenam Klu
RELATED COURSES
View all Courses
Keep Exploring
Related Courses
