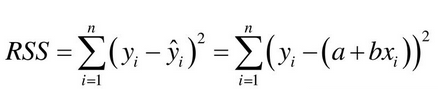The residual sum of squares
A residual sum of squares (RSS), also known as the sum of squared residuals (SSR), is a statistical technique used to measure the amount of variance in a data set that is not explained by a regression model. It is the sum of the squared values of the residuals (deviations of predicted from actual empirical values of data).
Forumula for SSR (or RSS)
is the actual value from data, is the predicted value using regression, and and are constants.
In the graph shown,
SSR is the total sum of the squares of these residuals (yellow lines).

Example
Given the set of values:
| 0 | 1 |
| 1 | 2 |
| 2 | 6 |
| 3 | 7 |
| 4 | 8 |
and with and , we will get the following result:
Free Resources
Copyright ©2025 Educative, Inc. All rights reserved