The rod cutting problem

Using dynamic programming

Since dynamic programming is mainly an optimization-over-plain recursion, we can use it to optimize the above exponential time algorithm. The idea is to store the results of subproblems so that we do not have to re-compute them when they are needed.

So, in the above example:

The possible range of length, of any sub-rod, is from 0 to 5. A sub-rod of a length within this range can be made.
We have 4 different prices of different-length sub-rods (i.e., cut marks, the place where cuts can be made on a sub-rod).

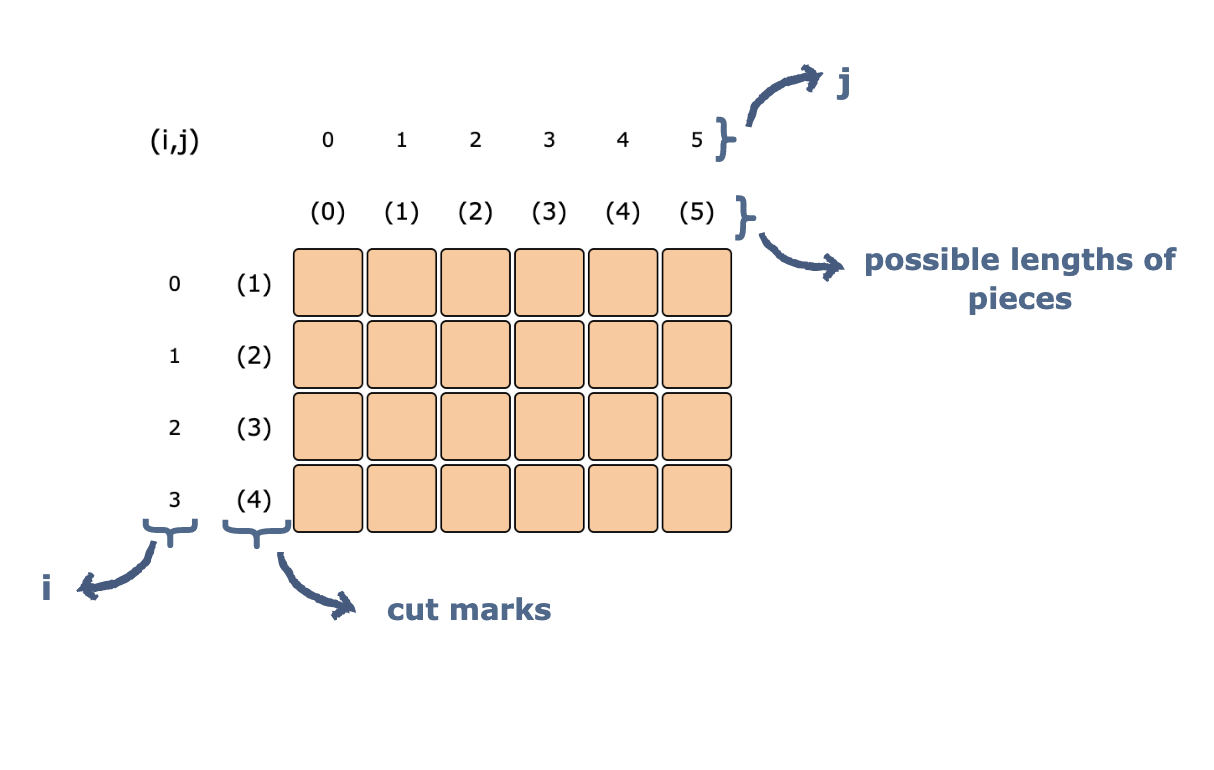
The grid above represents our sub-problems. Let:

i be the number of rows
j be the number of columns

The cell at [i,j] represents the maximum amount of profit that can be earned from selling a rod of initial length j. One is able to choose the cuts from an array of 0 to i.

For example, the cell at [2,3] represents the maximum profit that can be earned from a rod with length 3, and an array of different prices of different-length sub-rods(0 to 2).

Now, let’s start filling in the table/array.

Start with the simple calculations first. If a rod has a length of 0, what would the maximum profit be? It would be 0.

Now, let’s start to fill in the rows

In the first row, we only have the price 2 at a length of 1 in our array.
At index [0,1], putting a cut at 1 would give a profit of 2. No cut would give a profit of 2.
At index of [0,2], putting a cut at 1 would give a profit of 4 (2 rods with a length of 1, each with a price of 2). No cut would give a profit of 4 (not 5 because the price of 2 does not exist in the array yet!). Hence, 4 is the better option.
Do this for the whole first row.

Your grid should look like this now:

You may have observed that we’re deciding, at every step, whether the newly added cut mark ( i+1) increases the profit of the given rod j, or not. We decide this by taking the maximum of 2 things:

The maximum profit of the length before the cut mark was made (i.e., the value at [ i-1,j] ). This is a case where we don’t include the newly added cut mark.
price [i] + the maximum profit at length j-i-1 for the current array of prices (i.e., the value at [i, j-i-1]) would have already been computed before this computation. This is a case where we use the new cut mark for its effect on the profit.

So, the general expression used for filling the grid is:

# Using numpy arrays
import numpy as np
price = [2,5,7,8]
n = 5
# Make an initial grid of all zeros
T = np.zeros((len(price),n+1))
for i in range(0,len(price)):
    for j in range(0,n+1):
        # First column => 0 length of rod => 0 profit
        if j == 0:
            continue
        # First row => T[i-1,j] doesn't exist so just pick the second value
        elif i == 0:
            T[i,j] = price[i] + T[i, j-i-1]
        # where j <= i => T[i, j-i-1] doesn't exist so just pick the first value
        elif (j-i-1) < 0:
            T[i,j] = T[i-1,j]
        
        # using the whole expression
        else:
            T[i,j] = max(T[i-1,j], (price[i] + T[i, j-i-1]))
        
# Answer in the extreme bottom right cell
print "Maximum profit is", T[len(price)-1,n]

Learn in-demand tech skills in half the time

PRODUCTS

Mock Interview

New

Courses

Skill Paths

Projects

Assessments

The rod cutting problem

Problem statement

Using dynamic programming

Now, let’s start to fill in the rows