Trees vs. graphs

A graph is a collection of nodes where each node might point to other nodes. These nodes are connected to each other through a set of edges.

Graphs are similar to trees, but trees follow certain rules when it comes to their edges:

• A tree with N nodes will have (N-1) edges, one edge for each parent-child relationship. All nodes must be reachable from the root and there must be exactly one possible path from the root to a node.

• In graphs, there are no rules dictating the connection among the nodes. A graph contains a set of nodes and a set of edges, but these edges can connect nodes in any possible way. In fact, trees are actually a subset of graphs.

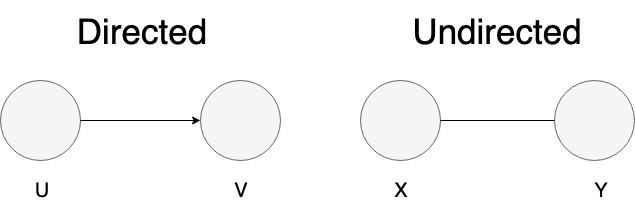
Edges can be of two types

1. Directed edges in which connections are one-wayUnidirectional. One of the endpoints is the origin and the other endpoint is the destination.
2. Undirected edges in which connections are two-wayBidirectional.

A directed edge can be represented using an ordered pair. For the above example, the ordered edge can be represented as (U, V), where the first element is the origin and the second element is the destination. For the ordered pair (U, V), we have a path from U to V; however, we do not have a path from V to U.

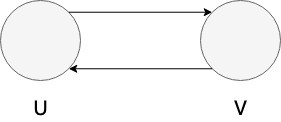
If we want a path from V to U, we need to draw another directed edge:

Here, the upper edge is (U, V) and the lower edge is (V, U). For undirected edges, the path is two-waybidirectional. Undirected edges are represented by unordered pairs {U, V}. Usually, all the edges in a graph are either directed or undirected, but it is possible to have a graph that contains a combination of both.

A graph in which all the edges are directed is called a Directed Graphs. Graphs in which all edges are undirected are called Undirected Graphs.

When are graphs used?

Many real-world systems are modeled using graphs. If you look at a social network (like Facebook), friendships can be represented by undirected graphs (if someone is your friend, you are also their friend).

However, there are other social networks, like Twitter and Instagram, that can be represented by directional graphs (you can follow someone but they do not necessarily follow you back). In order for the graph to be two-way, the person you follow would also have to click “follow” (or create an edge).

You can also use graphs to represent streets in order to get directions from one point to another. If all roads in an area are two-way streets, you may be able to get away with representing a map as an undirected graph. However, maps and directions are usually represented by directional graphs.

You can use graphs to calculate the shortest path from one point to another.

Weighted edges

Not all edges are created equal. Sometimes, in a graph, some connections may be preferable to others. Let’s go back to the example of representing streets as graphs. Usually, if you wanted to get from point A to point B, you would want to take the path with the least traffic as an edge with less traffic may be “worth more”. A highway with a higher speed limit may also be “worth more” than a side road with a lower speed limit.

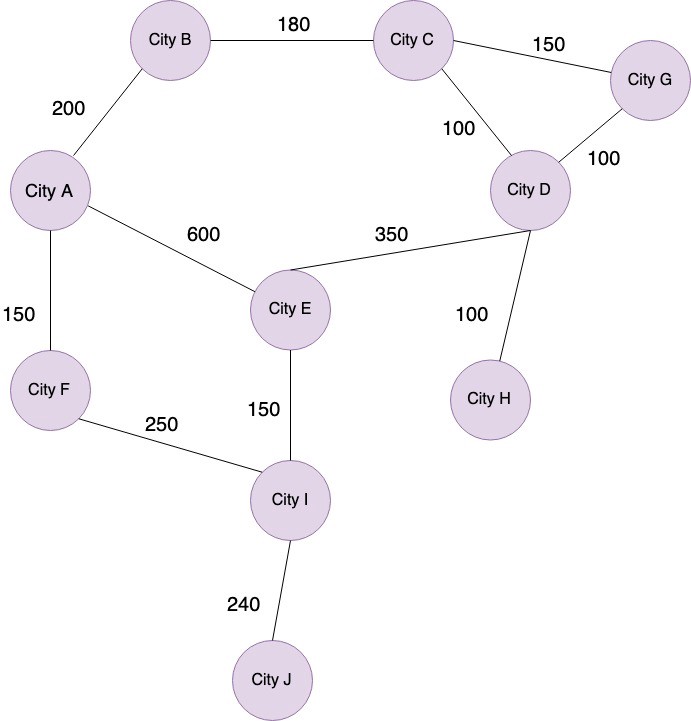
If we wanted to find the best path from City A to City H, we would have these options:

1. A → B → C → D → H = 200 + 180 + 100 + 100 = 580

2. A → B → C → G → D → H = 200 + 180 + 100 + 150 + 100 = 730

3. A → E → D → H = 600 + 350 + 100 = 1050

4. A → F→ I → E → D → H = 150 + 250 + 150 + 350 + 100 = 1000

If we assume the best path is the one with the highest weight, number 3 is the best option. It also happens to be the path with the least edges.

Graph traversal

There are two common ways to find the path from one node to another node in a graph:

1. [Depth First Search (DFS)[https://www.educative.io/answers/what-is-depth-first-search]

2. Breadth-First Search (BFS)

Depth First Search (DFS): Preorder or traverse all the way down a branch before moving on to the next. Visit a node, then visit one of its children, and continue to visit the children of its children until the end of a branch.

DFS can be implemented using recursion or iteration.

Breadth First Search (BFS): Level-order or traverse layer by layer. Visit a node, then visit all of its children before moving on to grandchildren. You can start BFS in a graph at any node you want. The node that you choose to start at is sometimes called the search key. You can visit any adjacent nodes (children) in any order that you like.

However, unlike trees, graphs may contain cyclesmeaning a node may be connected to a node that was already visited. To avoid processing a node more than once, you can use a boolean visited array. To implement BFS, you can use a queue data structure to keep track of nodes to visit before moving on to another layer.

Thanks for reading!