What are Activation Functions in Neural Networks?
Activation Functions are essential parts of neural networks. In this shot, we will be reviewing how neural networks operate to understand Activation Functions and we’ll go through some types of Activation Functions.
Overview of Neural Networks
Neural networks, also called artificial neural networks (ANNs), are a machine learning subset central to deep learning algorithms.
As their name suggests, they mimic how the human brain learns. The brain gets stimuli from the external environment, processes the information, and then provides an output. As the task becomes more difficult, numerous neurons form a complex network that communicates with one another.
The image above is a neural network with interconnected neurons. Each neuron is defined by its weight, bias, and activation function.
x =
Where do Activation Functions Come in?
Activation functions are essential components of neural networks because they introduce non-linearity. A neural network would be a linear regressor without activation functions. They determine whether a neuron should be fired. A non-linear transformation is applied to the input before it is sent to the next layer of neurons. Otherwise, the output is finalised.
x = Activation
Simply put, activation functions are like sensors that will trigger your brain neurons to recognize when you smell something pleasant or unpleasant.
The non-linear nature of most activation functions is intentional. Neural networks can compute arbitrarily complex functions using non-linear activation functions.
Types of Activation Functions
Activation Functions can be categorized into Linear and Non-Linear Activation Functions.
-
Linear Activation Functions are linear, so the output of the functions will not be confined between any range. They don’t affect the complexity of data that is fed to the neural networks.
-
Non-linear Activation Functions are the most popular because they allow the model to generalise or adapt to a wide range of variables while still distinguishing between the output.
Below is a brief overview of 3 common Activation Functions:
- Sigmoid: It is a non-linear activation function that is commonly utilised. It is S-shaped and transforms data in the range of 0 to 1.
Here’s the mathematical expression for sigmoids: =
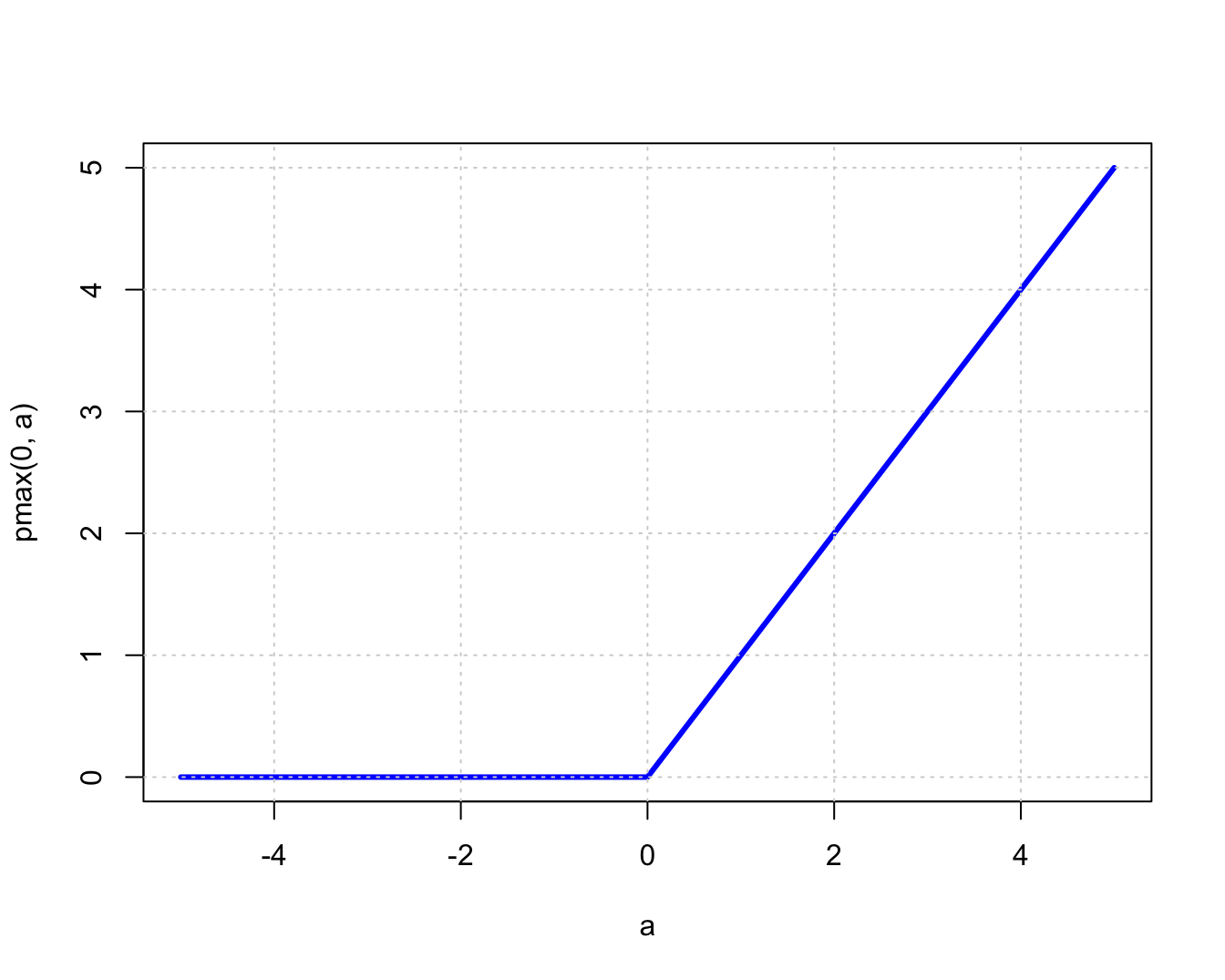
- Rectified Linear Unit (ReLU): It is the most used activation function globally because it is used in almost all convolutional neural networks or deep learning.
Here’s the mathematical expression for ReLU: =max(0,x), if x <= 0, otherwise x
- Hyperbolic Tangent (tanH): It is similar to the logistic sigmoid as it is also s-shaped. The range of the tanH function always lies between -1 and 1. tanh is also sigmoidal (s-shaped).
Here’s the mathematical expression for ReLU: = or =