What is Mahalanobis distance?

Mahalanobis distance is defined as the distance between a distribution and a point. It was introduced in 1936 by P. C. Mahalanobis.

Limitations of the Euclidean distance

As you might know, the Euclidean distance is simple and the most commonly used as metric to find distance. We use the Mahalanobis distance because there are several limitations of the Euclidean distance. These limitations are as follows:

• The Euclidean distance is very sensitive to the dataset's scales of features or variables. The Mahalanobis distance normalizes the variables, as large-scale variables may lead to inappropriate results.

• The result of the Euclidean distance is affected by the outliers, while on the other hand, the Mahalanobis distance finds the distribution of the dataset. It can ignore the outliers as well.

Mathematical intuition

The Mahalanobis distance takes account of the covariance and structure of the variables. The equation for calculating the Mahalanobis distance is given below.

$D(x) = \sqrt{(x - μ)' Σ^{(-1)} (x - μ)}$

In this equation:

• $x$ is the data point for which we want to calculate the distance.

• $μ$ is a mean vector of the distribution.

• $Σ$ is the covariance matrix.

• $'$ means taking the transpose of the matrix.

The term $(x-μ)$ ensures that the distribution is centered at the origin and $Σ^{-1}$indicates that variables are normalized by their variances. It considers the covariance and correlation of the variables, giving equal weight to all the variables.

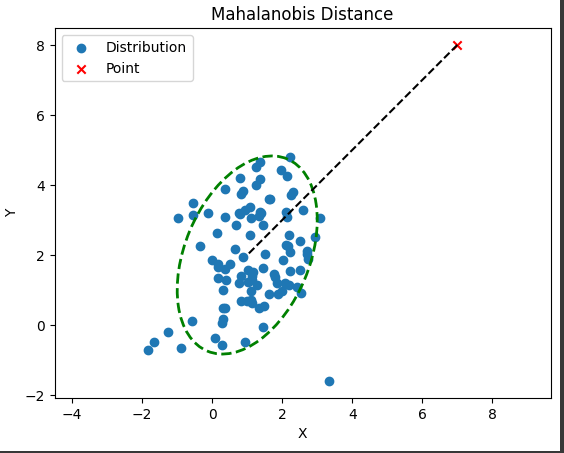
The below figure illustrates the Mahalanobis distance between the point and the distribution.

Applications

There are several applications of the Mahalanobis distance, which are discussed below.

• Mahalanobis distance is used to figure out the outliers in the data set. The points with large Mahalanobis distances are far from the distribution and considered outliers.

• Based on the characteristics of the variables, it is used to determine the similarity and dissimilarity of the points with the clusters.

• In terms of deep learning, it is used to find anomaly detection with the help of outliers.

Conclusion

In this Answer, we discussed the mathematical intuition and applications of the Mahalanobis distance. We also looked at the limitations of the Euclidean distance and how the Mahalanobis distance is better than it.

Note: Here is the link, if you want to learn about Manhattan distance.

To test your understanding of the Mahalanobis distance, try to solve this quiz.