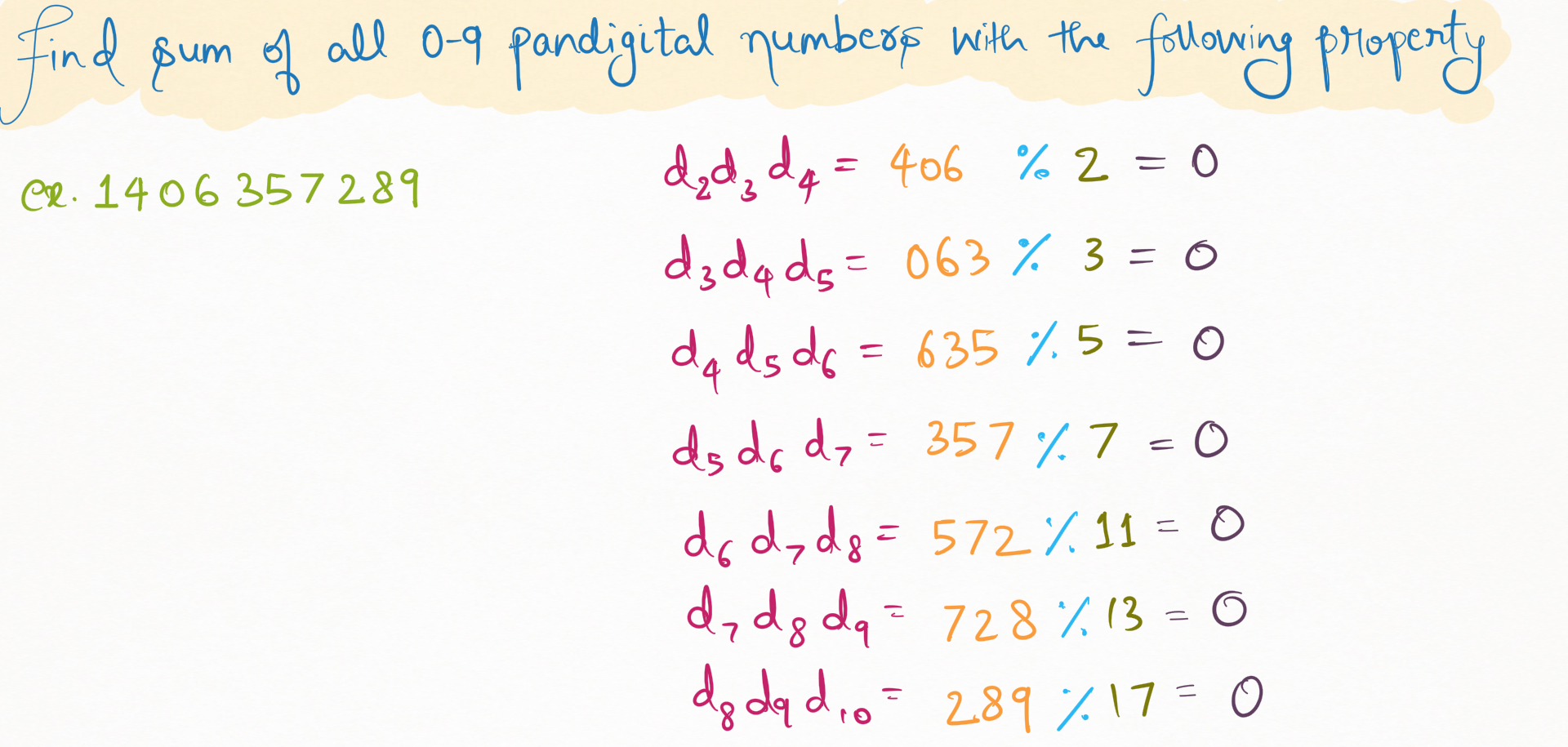What is Project Euler 43 sub-string divisibility?
The number 1406357289, rather than just being a 0-9 pan-digital number, also has an interesting property:
(d2d3d4)%2==0
(d3d4d5)%3==0
(d4d5d6)%5==0
(d5d6d7)%7==0
(d6d7d8)%11==0
(d7d8d9)%13==0
(d8d9d10)%17==0
We can find the sum of all such 0-9 pan-digital numbers with this property, as demonstrated below:
Question Analysis
Solution approach
A simple brute force approach with slight optimization would work seamlessly here. We will iterate through each permutation of 0-9 pan-digital number and check condition for each of them.
Optimization
- For
d2d3d4to be even,d4must be even. - For
d4d5d6to be a multiple of 5,d6must be 0 or 5.
Code Implementation
"""Coded by - Armaan Nougai"""from itertools import permutationsdatas=list(map(lambda j: ''.join(j) ,list(permutations('0123456789'))))ans=0for number in datas:if int(number[3])%2==0 and int(number[5])%5==0:if int(number[1:4])%2==0 and int(number[2:5])%3==0 and int(number[3:6])%5==0 and int(number[4:7])%7==0 and int(number[5:8])%11==0 and int(number[6:9])%13==0 and int(number[7:10])%17==0:ans+=int(number)print(ans)