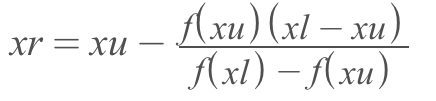What is the false position method in Python?
Finding the roots of complicated equations is very difficult, and sometimes impossible, so we are forced to use graphical methods. We use graphical methods to approximate the root by performing a defined set of calculations over multiple iterations. This means that we approximate more accurately and get closer to the actual root with each iteration.
The false position method is an algorithm that uses the value of the previous estimate to estimate a value that’s closer to the actual value. The false position method does this over multiple iterations and keeps the root of the function bracketed.
How to use the algorithm
-
We select the upper and lower values in which the actual root might lie.
-
We label the upper root as
“xu”and the lower root as“xl”. -
We calculate the estimated root with the following formula, where
xris the new root.To check whether the actual root lies in the
xl-xrorxr-xuintervals, we use the formulaf(xl)*f(xr). -
If the answer to the above identity is negative, the root is present in this interval.
xrbecomes the newxu, whilexlremains the same. This iteration is now complete, and the process starts again. -
If the answer to the above identity is positive, the root is present in the upper interval.
xrnow becomes the newxl, whilexuremains the same. This iteration is now complete, and the process starts again. -
If the answer to the above identity is zero, the root is equal to
xrand the process is terminated.
import mathdef func(x):func = 0.95*(pow(x,3))-5.9*(pow(x,2))+10.9*x-6 #Example equationreturn funcdef false_position():ea = 100 #Absolute errorxl = 3 #Lower limitxu = 4 #Upper limitxold=0i=1while ea > 0.1: #This loop runs until the absolute error becomes less than 0.1.xr = xu - (func (xu) * (xl - xu) / (func (xl) - func (xu))) #xr is the estimated root.ea = ((xr - xold) / xr) * 100 #Re-computing error: This takes the error from the previous estimation.sign_check=func(xr) * func(xl) #As mentioned in the algorithm above, this is done to determine the whixh interval has the root.if sign_check < 0: #Check where the root lies, as entioned in the algorithm above.xu = xrelse:xl = xrxold = xr #xold stores the previous value of xr to find absolute error.print("Iteration",i)print("Absolute Error", ea)print("Root",xr)i=i+1def main():false_position()main()