Find the Inner Product of Two Quantum States Using the SWAP Test

As the technology employed in quantum computing is fundamentally different from classical computing technology, it requires an altogether different class of algorithms for implementing computational tasks. In fact, quantum algorithms is one of the most active areas of research in quantum computing.

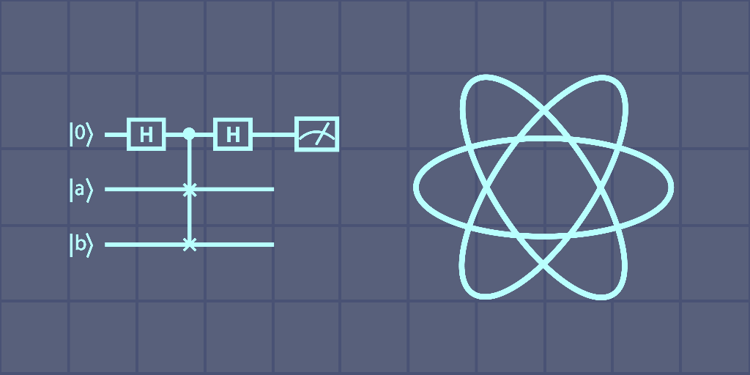
The SWAP test is a quantum algorithm used to find the similarity between two quantum states encoded on a quantum circuit. Apart from the quantum state registers, the SWAP test has a single qubit which, after the implementation of certain quantum operations, is measured to determine the results. The results of performing the SWAP test on the quantum states $\vert a\rangle$ and $\vert b\rangle$ are described by the following two equations:

$$P\vert0\rangle = \frac{1}{2} + \frac{1}{2}\langle a\vert b\rangle ^2$$

$$P\vert1\rangle = \frac{1}{2} - \frac{1}{2}\langle a\vert b\rangle ^2$$

Here, $P\vert0\rangle$ and $P\vert1\rangle$ are the probabilities of getting the states $\vert0\rangle$ and $\vert1\rangle$ respectively after measurement.

Therefore, by using the SWAP test, we can determine the inner product and the similarity of two quantum states by using the following formula:

$$\langle a\vert b\rangle = \sqrt{2 P\vert0\rangle - 1}$$