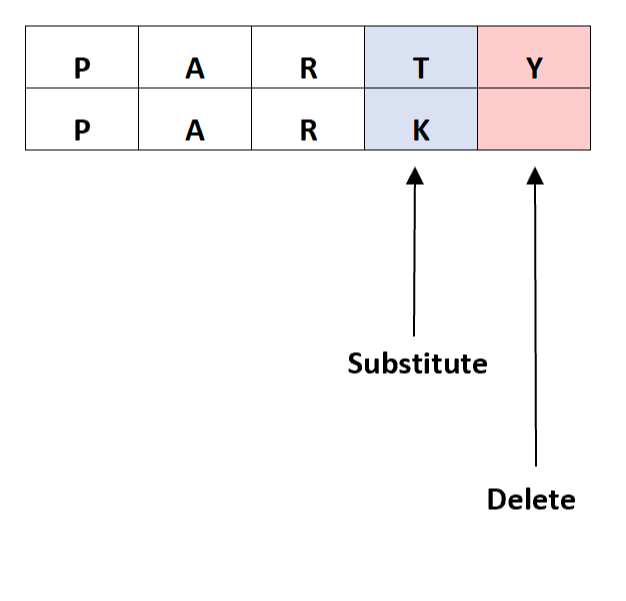
The Levenshtein distance algorithm
The Levenshtein distance (a.k.a edit distance) is a measure of similarity between two strings. It is defined as the minimum number of changes required to convert string a into string b (this is done by inserting, deleting or replacing a character in string a). The smaller the Levenshtein distance, the more similar the strings are. This is a very common problem in the application of Dynamic Programming.
Explanation
Using sub-problems
A pre-requisite for applying Dynamic Programming, to solve a problem, is to demonstrate that the solution to the original problem can be found by using the solutions to the sub-problems.
The approach here is somewhat simple and intuitive. Consider the strings a and b up to their last character:
- If the last characters of both strings are the same, then the edit distance is equal to the edit distance of the same two strings, up to their second-to-last character.
- If the last character is different, then the edit distance is equal to the minimum of the cost of inserting, deleting, or replacing the last character of string
a.
Understanding the array
Since DP utilises memory for storing the solutions to sub-problems, we will use a 2D array (D) for this purpose.
The value in D[i][j] represents the edit distance if we consider the strings a and b, till their ith and jth character, respectively. Therefore, the answer to the original problem will be found in D[length of 'a'][length of 'b'].
Code
#include <iostream>#include <cstring>#include <algorithm>using namespace std;int findMin(int x, int y, int z){if(x <= y && x <= z)return x;else if(y <=x && y <= z)return y;elsereturn z;}void freeMemory(int** arr, int a, int b){for(int i = 0; i < a; i++){delete[] arr[i];}delete[] arr;}int findDistance(char a[], char b[]){// Declaring a 2D array on the heap dynamically:int len_a = strlen(a);int len_b = strlen(b);int** d = new int*[len_a + 1];for(int i = 0; i < len_a + 1; i++)d[i] = new int[len_b + 1];// Initialising first column:for(int i = 0; i < len_a + 1; i++)d[i][0] = i;// Initialising first row:for(int j = 0; j < len_b + 1; j++)d[0][j] = j;// Applying the algorithm:int insertion, deletion, replacement;for(int i = 1; i < len_a + 1; i++){for(int j = 1; j < len_b + 1; j++){if(a[i - 1] == b[j - 1]){d[i][j] = d[i - 1][j - 1];}else{// Choosing the best option:insertion = d[i][j - 1];deletion = d[i - 1][j];replacement = d[i - 1][j - 1];d[i][j] = 1 + findMin(insertion, deletion, replacement);}}}int answer = d[len_a][len_b];freeMemory(d, len_a + 1, len_b + 1);return answer;}int main() {char a[] = "Carry";char b[] = "Bark";cout << "Levenshtein Distance: " << findDistance(a, b);return 0;}
Free Resources