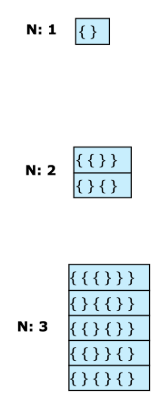
All Possible Braces
Problem Statement
Print all braces combinations for a given value n so that they are balanced. Here are a few examples:
Hint
- Recursion
Try it yourself
vector<vector<char>> print_all_braces(int n) {
//TODO: Write - Your - Code
vector<vector<char>> result;
return result;
}Solution
void print(vector<vector<char>> result){
for(int i = 0; i < result.size(); i++){
cout << "[ ";
for(int j = 0; j < result[i].size(); j++){
cout << result[i][j] << ", ";
}
cout << "]" << endl;
}
}
void print_all_braces_rec(
int n,
int left_count,
int right_count,
vector<char>& output, vector<vector<char>>& result) {
if (left_count == n && right_count == n) {
result.push_back(output);
}
if (left_count < n) {
output.push_back('{');
print_all_braces_rec(n, left_count + 1, right_count, output, result);
output.pop_back();
}
if (right_count < left_count) {
output.push_back('}');
print_all_braces_rec(n, left_count, right_count + 1, output, result);
output.pop_back();
}
}
vector<vector<char>> print_all_braces(int n) {
vector<vector<char>> result;
vector<char> output;
print_all_braces_rec(n, 0, 0, output, result);
return result;
}
int main() {
vector<vector<char>> result = print_all_braces(3);
print(result);
}Solution Explanation
Runtime complexity
The runtime complexity of this solution is exponential,
Memory complexity
The memory complexity of this solution is linear, O(n).
Solution Breakdown
The solution is to maintain counts of left_braces and right_braces. The basic algorithm is as follows:
left_braces count: 0
right_braces count: 0
if left_braces count is less than n:
add left_braces and recurse further
if right_braces count is less than left_braces count:
add right_braces and recurse further
stop recursing when left_braces and right_braces counts are both equal to n
SOLUTIONS
SOLUTIONS
SOLUTIONS
