Clone a Directed Graph

Table of Contents

Problem Statement Hint Try it yourself Solution Solution Explanation Runtime Complexity Memory Complexity Solution Breakdown

Home/

Blog/

Interview Prep/

Clone a Directed Graph

1 min read

Oct 15, 2025

Problem Statement#

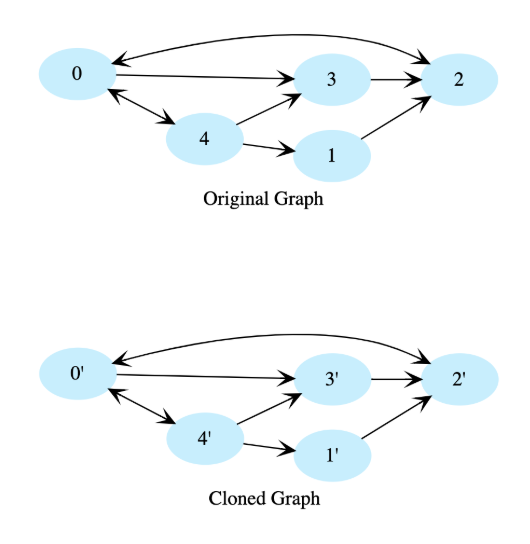
Given the root node of a directed graph, clone this graph by creating its deep copy so that the cloned graph has the same vertices and edges as the original graph.

Let’s look at the graphs below as an example. If the input graph is G = (V, E) where V is set of vertices and E is set of edges, then the output graph (cloned graph) G’ = (V’, E’) such that V = V’ and E = E’.

Note: We are assuming that all vertices are reachable from the root vertex. i.e. we have a connected graph.

struct Node {
  int data;
  list<Node*> neighbors;
  Node(int d) : data(d) {}
};
Node* clone_rec(Node* root, 
        unordered_map<Node*, 
        Node*>& nodes_completed) {
  
  if (root == nullptr) {
    return nullptr;
  }
  Node* pNew = new Node(root->data);
  nodes_completed[root] = pNew;
  
  for (Node* p : root->neighbors) {
    
    auto x = nodes_completed.find(p);
    
    if (x == nodes_completed.end()){
      pNew->neighbors.push_back(clone_rec(p, nodes_completed));
    } else {
      pNew->neighbors.push_back(x->second /*value*/);
    }
  }
  
  return pNew;
}
Node* clone(Node* root) {
  unordered_map<Node*, Node*> nodes_completed;
  return clone_rec(root, nodes_completed);
}
// this is un-directed graph i.e.
// if there is an edge from x to y
// that means there must be an edge from y to x
// and there is no edge from a node to itself
// hence there can maximim of (nodes * nodes - nodes) / 2 edgesin this graph
void create_test_graph_undirected(int nodes, int edges, vector<Node*>& vertices) {
  for (int i = 0; i < nodes; ++i) {
    vertices.push_back(new Node(i));
  }
  vector<pair<int, int>> all_edges;
  for (int i = 0; i < vertices.size(); ++i) {
    for (int j = i + 1; j < vertices.size(); ++j) {
      all_edges.push_back(pair<int, int>(i, j));
    }
  }
  std::random_shuffle(all_edges.begin(), all_edges.end());
  for (int i = 0; i < edges && i < all_edges.size(); ++i) {
    pair<int, int>& edge = all_edges[i];
    vertices[edge.first]->neighbors.push_back(vertices[edge.second]);
    vertices[edge.second]->neighbors.push_back(vertices[edge.first]);
  }
}
void print_graph(vector<Node*>& vertices) {
  for (Node* n : vertices) {
    cout << n->data << ": {";
    for (Node* t : n->neighbors) {
      cout << t->data << " ";
    }
    cout << "}" << endl;
  }
}
void print_graph(Node* root, unordered_set<Node*>& visited_nodes) {
  if (root == nullptr || visited_nodes.find(root) != visited_nodes.end()) {
    return;
  }
  visited_nodes.insert(root);
  cout << root->data << ": {";
  for (Node* n : root->neighbors) {
    cout << n->data << " ";
  }
  cout << "}" << endl;
  for (Node* n : root->neighbors) {
    print_graph(n, visited_nodes);
  }
}
void print_graph(Node* root) {
  unordered_set<Node*> visited_nodes;
  print_graph(root, visited_nodes);
}
int main() {
  vector<Node*> vertices;
  create_test_graph_undirected(7, 18, vertices);
  
  print_graph(vertices[0]);
  Node* cp = clone(vertices[0]);
  cout << endl << "After copy" << endl;
  print_graph(cp);
  
  return 0;
}

Solution Explanation#

Runtime Complexity#

Linear, O(n).

Memory Complexity#

Logarithmic, O(n). ‘n’ is the number of vertices in the graph.

Solution Breakdown#

We use depth-first traversal and create a copy of each node while traversing the graph. To avoid getting stuck in cycles, we’ll use a hashtable to store each completed node and will not revisit nodes that exist in the hashtable. The hashtable key will be a node in the original graph, and its value will be the corresponding node in cloned graph.