Problem Statement#
Given the root to a binary tree where each node has an additional pointer called sibling (or next), connect the sibling pointer to the next node in the same level. The last node in each level should point to the first node of the next level in the tree.
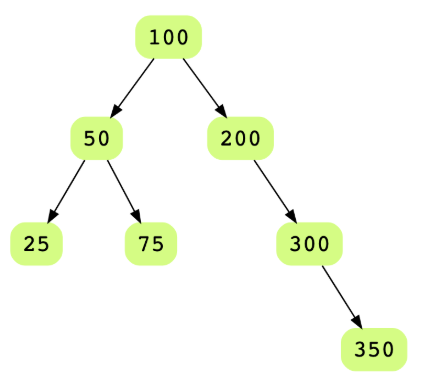
Consider the following binary tree.
Here’s how the final tree would look when all sibling pointers have been connected.
void populate_sibling_pointers(BinaryTreeNode* root) {//TODO: Write - Your - Code}
Solution#
void populate_sibling_pointers(BinaryTreeNode* root) {if (root == nullptr) {return;}BinaryTreeNode* current = root;BinaryTreeNode* last = root;while (current != nullptr) {if (current->left != nullptr) {last->next = current->left;last = current->left;}if (current->right != nullptr) {last->next = current->right;last = current->right;}last->next = nullptr;current = current->next;}}void reset_siblings(BinaryTreeNode* root) {if (root == nullptr) return;root->next = nullptr;reset_siblings(root->left);reset_siblings(root->right);}int main(int argc, char* argv[]) {BinaryTreeNode* root = create_random_BST(15);display_level_order(root);cout << endl << "level_order_using_next";level_order_using_next(root);cout << endl;reset_siblings(root);populate_sibling_pointers(root);level_order_using_next(root);}
Solution Explanation#
Runtime Complexity#
Linear, O(n).
Memory Complexity#
Constant O(1).
Solution Breakdown#
A binary tree is a data structure made up of nodes, where each node contains a “left” reference, a “right” reference, and a data element. The topmost node in the tree is called the root. Every node except the ‘root’ node is connected by a directed edge from exactly one other node. This node is called the parent of that node. On the other hand, each node can be connected to an arbitrary number of nodes, called children. Nodes with the same parent node are called siblings.
Each node in the above binary tree has one more pointer, i.e., next, along with the left and right pointers. ‘Next’ is used to connect one node to the other. After connecting siblings, a linked-list-like structure is formed whose head is the root node. We keep two pointers, current and last. ‘current’ is the node we are working at, and ‘last’ is the last node in the linked list already constructed (i.e., siblings already connected). Below are the steps we use to connect all siblings in the tree:
Initially set both current and last as 'root'while current node is not nullIf current node has a left child, append this left node to the last and make it last node.If current node has a right child, append this right node to the last and make it last node.update current node to current's next node
Practice problems like this and many more by checking out our Grokking the Coding Interview: Patterns for Coding Questions course!
Free Resources