Find Low/High Index

Problem Statement

Given a sorted array of integers, return the low and high index of the given key. You must return -1 if the indexes are not found.

The array length can be in the millions with many duplicates.

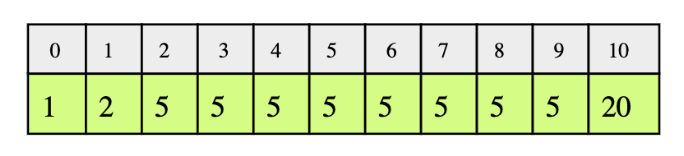
In the following example, according to the the key, the low and high indices would be:

key: 1, low = 0 and high = 0
key: 2, low = 1 and high = 1
key: 5, low = 2 and high = 9
key: 20, low = 10 and high = 10

int find_low_index(vector<int>& arr, int key) {
  int low = 0;
  int high = arr.size() - 1;
  int mid = high / 2;
  while (low <= high) {
    int mid_elem = arr[mid];
    if (mid_elem < key) {
      low = mid + 1;
    }
    else {
      high = mid - 1;
    }
    mid = low + (high - low) / 2;
  }
  if (low < arr.size() && arr[low] == key) {
    return low;
  }
  return -1;
}
int find_high_index(vector<int>& arr, int key) {
  int low = 0;
  int high = arr.size()-1;
  int mid = high/2;
  while (low <= high) {
    int mid_elem = arr[mid];
    if (mid_elem <= key) {
      low = mid+1;
    }
    else {
      high = mid-1;
    }
    mid = low + (high-low)/2;
  }
  
  if(high == -1)
    return high;
  
  if (high < arr.size() && arr[high] == key) {
    return high;
  }
  return -1;
}
int main(int argc, char* argv[]) {
  {
    vector<int> arr = {1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 6, 6};
    int key = 5;
    int low = find_low_index(arr, key);
    int high = find_high_index(arr, key);
    cout << "Low Index of " << key << ": " << low <<endl;
    cout << "High Index of " << key << ": "<< high <<endl;
    
    key = -2;
    low = find_low_index(arr, key);
    high = find_high_index(arr, key);
    cout << "Low Index of " << key << ": "<< low <<endl;
    cout << "High Index of " << key << ": "<< high <<endl;
  }
}

Solution Explanation

Runtime complexity

Since we are using binary search, the runtime complexity is logarithmic, O(logn).

Memory complexity

The memory complexity is constant, O(1) since no extra storage is being used.

Solution Breakdown

Linearly scanning the sorted array for low and high indices are highly inefficient since our array size can be in millions.

Instead, we will use a slightly modified binary search to find the low and high indices of a given key.

We need to do binary search twice;

once for finding the low index.
once for finding the high index.

Low index

Let’s look at the algorithm for finding the low index:

At every step, consider the array between low and high indices and calculate the mid index.
If the element at mid index is less than the key, low becomes mid + 1 (to move towards the start of range).
If the element at mid is greater or equal to the key, the high becomes mid - 1. Index at low remains the same.
When low is greater than high, low would be pointing to the first occurrence of the key.
If the element at low does not match the key, return -1.

High index

Similarly, we can find the high index by slightly modifying the above condition:

switch the low index to mid + 1 when element at mid index is less than or equal to the key.
switch the high index to mid - 1 when the element at mid is greater than the key.