Find Maximum Single Sell Profit
Problem Statement
Given a list of daily stock prices (integers for simplicity), return the buy and sell prices for making the maximum profit.
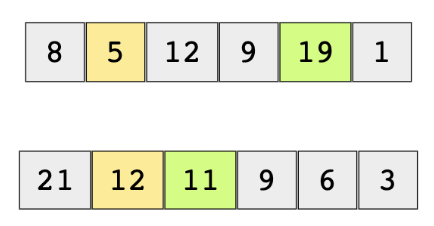
We need to maximize the single buy/sell profit. If we can’t make any profit, we’ll try to minimize the loss. For the below examples, buy (orange) and sell (green) prices for making a maximum profit are highlighted.
Hint
- Use Kadane’s algorithm
Try it yourself
tuple<int, int> find_buy_sell_stock_prices(int* array, int size) {//TODO: Write - Your - Codetuple<int, int> result(std::make_pair(-1, -1));return result; // t is a tuple with (high, low) price values}
Solution
tuple<int, int> find_buy_sell_stock_prices(int* array, int size) {if(array == NULL || size < 2) {tuple<int, int> t(std::make_pair(NULL, NULL));return t;}int current_buy = array[0];int global_sell = array[1];int global_profit = global_sell - current_buy;int current_profit = -2147483648; //INT_MINfor(int i = 1; i < size; i++) {current_profit = array[i] - current_buy;if(current_profit > global_profit) {global_profit = current_profit;global_sell = array[i];}if(current_buy > array[i]) {current_buy = array[i];}}tuple<int, int> result(std::make_pair(global_sell - global_profit, //buy priceglobal_sell //sell price));return result;}int main() {int array[] = {1, 2, 3, 4, 3, 2, 1, 2, 5};tuple<int, int> result;result = find_buy_sell_stock_prices(array, 9);cout << "Buy Price: "<< get<0>(result) << ", Sell Price: " << get<1>(result) << endl;int array2[] = {8, 6, 5, 4, 3, 2, 1};result = find_buy_sell_stock_prices(array2, 7);cout << "Buy Price: " << get<0>(result) << ", Sell Price: " << get<1>(result) << endl;}
Solution Explanation
Runtime complexity
The runtime complexity of this solution is linear, O(n).
Memory complexity
The memory complexity of this algorithm is constant, O(1).
Solution Breakdown
The values in the array represent the cost of a stock each day. As we can buy and sell the stock only once, we need to find the best buy and sell prices for which our profit is maximized (or loss is minimized) over a given span of time.
A naive solution, with runtime complexity of , is to find the maximum gain between each element and its succeeding elements.
There is a tricky linear solution to this problem that requires maintaining current_buy_price (which is the smallest number seen so far), current_profit, and global_profit as we iterate through the entire array of stock prices. At each iteration, we will compare the current_profit with the global_profit and update the global_profit accordingly.
The basic algorithm is as follows:
current profit = INT_MIN
current buy = stock_prices[0]
global sell = stock_prices[1]
global profit = global sell - current buy
for i = 1 to stock_prices.length:
current profit = stock_prices[i] - current buy
if current profit is greater than global profit
then update global profit to current profit and update global sell to stock_prices[i]
if stock_prices[i] is less than current buy
then update current buy to stock_prices[i]
return global profit and global sell
Practice problems like this and many more by checking out our Grokking the Coding Interview: Patterns for Coding Questions course!