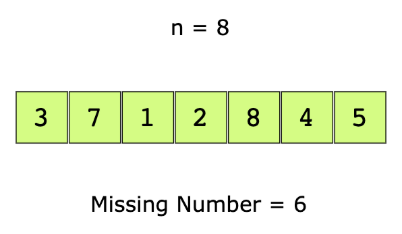
Find the Missing Number
Problem Statement
You are given an array of positive numbers from to , such that all numbers from to are present except one number, . You have to find . The input array is not sorted.
For example, let’s look at the below array.
Hint
- How would you calculate the sum of numbers from to ?
Try it yourself
#include <iostream>#include <vector>using namespace std;int FindMissing(const vector<int>& input) {//TODO: Write - Your - Codereturn -1;}
Solution
#include <iostream>#include <vector>#include <string>#include <numeric>using namespace std;int FindMissing(const vector<int>& input) {// Calculate sum of all elements in the input vector// The accumulate function can this for usint actual_sum = accumulate(input.begin(), input.end(), 0);int n = input.size();// Find the sum of first n numbers using the arithmetic series sum formula,// i.e., (n∗(n+1))/2int sum_of_n = (n * (n + 1)) / 2;// The difference between sum_of_n and actual_sum, is the missing number in the// arrayreturn sum_of_n - actual_sum;}int main() {vector<vector<int> > vec_list = {{0}, {3, 7, 1, 2, 0, 4, 5}, {9, 6, 4, 2, 3, 5, 7, 0, 1}};for (int i = 0; i < vec_list.size(); i++) {cout << i + 1 << ". Original ";// A custom function to print the vectorPrintList(vec_list[i]);int missing = FindMissing(vec_list[i]);cout << " The missing number is: " << missing << endl;cout << "\n------------------------------------------------------------------------------------------------------\n" << endl;}}
Solution Explanation
Runtime Complexity
Linear, .
Memory Complexity
Constant, .
Solution Breakdown
A naive solution is to simply search for every integer between 1 and n in the input array, stopping the search as soon as there is a missing number. Since the input array is not sorted, its time complexity will be ).
Can you do better than )? Yes.
You could sort the array and then do a linear scan ) where you compare all consecutive elements to find the missing number. However, the time complexity of this algorithm is ) due to the time spent in sorting.
You can do better. Here is a linear, ), solution that uses the arithmetic series sum formula.
Here are the steps to find the missing number.
- Find the sum of elements of all the numbers in the array. Let’s call it
sum. This would require a linear scan, . - Then find the expected sum of the first numbers using the formula: . Let’s call it
total. - The difference between
totalandsumis the missing number in the array.
Practice problems like this and many more by checking out our Grokking the Coding Interview: Patterns for Coding Questions course!