Is Binary Tree a Binary Search Tree?
Problem Statement
Given a Binary Tree, figure out whether it’s a Binary Search Tree. In a binary search tree, each node’s key value is smaller than the key value of all nodes in the right subtree, and are greater than the key values of all nodes in the left subtree i.e. L < N < RL<N<R.
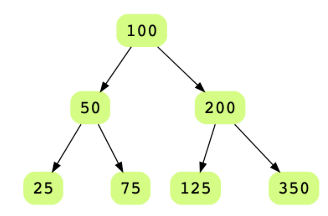
Below is an example of binary tree that is a valid BST.
Below is an example of a binary tree that is not a BST
Hint
- Recursion
- Inorder traversal
Try it yourself
bool is_bst(BinaryTreeNode* root) {//TODO: Write - Your - Codereturn false;}
Solution
bool is_bst_rec(BinaryTreeNode* root,int min_value,int max_value) {if (root == nullptr) {return true;}if (root->data < min_value ||root->data > max_value) {return false;}returnis_bst_rec(root->left, min_value, root->data) &&is_bst_rec(root->right, root->data, max_value);}bool is_bst(BinaryTreeNode* root) {returnis_bst_rec(root,numeric_limits<int>::min(),numeric_limits<int>::max());}void test_is_bst() {BinaryTreeNode* root = create_random_BST(15);BinaryTreeNode* root2 = create_BinaryTree(20);root2->left = root;root2->right = root;display_level_order(root);display_level_order(root2);assert(is_bst(root));assert(!is_bst(root2));}int main(int argc, char* argv[]) {test_is_bst();}
Solution Explanation
Runtime Complexity
The runtime complexity of this solution is linear, O(n).
Memory Complexity
The memory complexity of this solution is linear, O(n).
Solution Breakdown
There are several ways of solving this problem. A basic algorithm would be to check on each node where the maximum value of its left sub-tree is less than the node’s data and the minimum value of its right sub-tree is greater than the node’s data. This is highly inefficient as for each node, both of its left and right sub-trees are explored.
Another approach would be to do a regular in-order traversal and in each recursive call, pass maximum and minimum bounds to check whether the current node’s value is within the given bounds. This approach is efficient compared to the one above.
Practice problems like this and many more by checking out our Grokking the Coding Interview: Patterns for Coding Questions course!