# Problem Statement
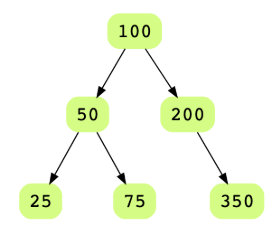
Given the root of a binary tree, display the node values at each level. Node values for all levels should be displayed on separate lines. Let’s take a look at the below binary tree.

Level order traversal for this tree should look like: 100; 50, 200; 25, 75, 350

<br>

## Hint
* Breadth first traversal

<br>

## Try it yourself

def level_order_traversal(root):
  result = ""
  #TODO: Write - Your - Code
  return result

import os, sys
utils_path = os.path.join('..', '..', '..', '..', 'problems', 'utils', 'python')
sys.path.append(utils_path)
from collections import deque

class BinaryTreeNode:
  def __init__(self, data):
    self.data = data
    self.left = None
    self.right = None
    self.next = None
    self.parent = None


import random

def insert_binary_tree(root, d):
  pNew = BinaryTreeNode(d)
  if root == None:
    return pNew

  parent = None
  pTemp = root
  while (pTemp != None): 
    parent = pTemp
    if d < pTemp.data:
      pTemp = pTemp.left
    else:
      pTemp = pTemp.right

  if d <= parent.data:
    parent.right = pNew
  else:
    parent.left = pNew

  return root

def insert(root, d):
  pNew = BinaryTreeNode(d)
  if root == None:
    return pNew

  parent = None
  pTemp = root
  while (pTemp != None): 
    parent = pTemp
    if d < pTemp.data:
      pTemp = pTemp.left
    else:
      pTemp = pTemp.right

  if d < parent.data:
    parent.left = pNew
  else:
    parent.right = pNew

  return root

def find_in_bst(root, d):
  if root == None:
    return None

  if root.data == d:
    return root
  elif root.data > d:
    return find_in_bst(root.left, d)
  else:
    return find_in_bst(root.right, d)

# find node in inorder 
# works for both BST and binary tree
def find_node(root, d):
  if root == None:
    return

  if root.data == d:
    return root

  temp = find_node(root.left, d)
  if temp != None:
    return temp

  return find_node(root.right, d) 

def display_inorder(node):
  if node == None:
    return

  display_inorder(node.left)
  print(str(node.data), end = ", ")
  display_inorder(node.right)

def create_BST(arr):
  root = None
  for x in arr:
    root = insert(root, x)
  return root

def create_binary_tree(count):
  root = None
  for i in range(1, count):
    root = insert_binary_tree(root, random.randrange(1,100))
  return root

def create_random_BST(count):
  root = None;
  for i in range(1, count):
    root = insert(root, random.randrange(200, 300))
  return root

def bst_to_list_rec(root, lst):
  if root == None:
    return

  bst_to_list_rec(root.left, lst)
  lst.append(root.data)
  bst_to_list_rec(root.right, lst)

def bst_to_list(root):
  lst = []
  bst_to_list_rec(root, lst)
  return lst

def insert_at_head(head, data):
  newNode = LinkedListNode(data)
  newNode.next = head
  return newNode

def populate_parents_rec(root, parent):
  if root == None:
    return 
  root.parent = parent

  populate_parents_rec(root.left, root)
  populate_parents_rec(root.right, root)

def populate_parents(root):
  populate_parents_rec(root, None)

def display_level_order(root):
  if root == None:
    return
  q = deque()
  q.append(root)

  while q:
    temp = q.popleft()
    print(str(temp.data) + ",", end = " ")
    if temp.left != None:
      q.append(temp.left)
    if temp.right != None:
      q.append(temp.right)

  print

def get_level_order(root):
  output = []
  if root == None:
    return output
  
  q = deque()
  q.append(root)

  while q:
    temp = q.popleft()
    output.append(temp.data)
    if temp.left != None:
      q.append(temp.left)
    if temp.right != None:
      q.append(temp.right)

  return output

def get_inorder_helper(root, output):
  if root == None:
    return output

  output = get_inorder_helper(root.left, output)
  output.append(root.data)
  output = get_inorder_helper(root.right, output)
  
  return output

def get_inorder(root):
  output = []
  return get_inorder_helper(root, output)

def is_identical_tree(root1,root2):
  if root1 == None and root2 == None:
    return True

  if root1 != None and root2 != None and root1.data == root2.data: 
    return is_identical_tree(root1.left,root2.left) and is_identical_tree(root1.right,root2.right)

  return False

Python

class LevelOrderTraversal{
    
  public static String levelOrderTraversal(BinaryTreeNode root) {
      //TODO: Write - Your - Code
        return "";
  }
} 

import java.util.*;
import java.math.*;

class BinaryTreeNode
{
    public int data;
    public BinaryTreeNode left;
    public BinaryTreeNode right;

    // below data members used only for some of the problems
    public BinaryTreeNode next;
    public BinaryTreeNode parent;
    public int count;

    public BinaryTreeNode(int d) {
      data = d;
      left = null;
      right = null;
      parent = null;
      count = 0;
    }
}
class BinaryTree {

public static BinaryTreeNode root;

public BinaryTree() {
  root = null;
}

public BinaryTree(BinaryTreeNode head) {
  this.root = head;
}

public static BinaryTreeNode insert(BinaryTreeNode root, int d) {

  BinaryTreeNode pNew = new BinaryTreeNode(d);
  if (root == null) {
    return pNew;
  }

  BinaryTreeNode parent = null;
  BinaryTreeNode pTemp = root;
  while (pTemp != null) {
    parent = pTemp;
    if (d <= pTemp.data) {
      pTemp = pTemp.left;
    } else {
      pTemp = pTemp.right;
    }
  }

  if (d <= parent.data) {
    parent.left = pNew;
    pNew.parent = parent;
  } else {
    parent.right = pNew;
    pNew.parent = parent;
  }  
  return root;
}

public static BinaryTreeNode insert_BT(BinaryTreeNode root, int d) {

  BinaryTreeNode pNew = new BinaryTreeNode(d);
  if (root == null) {
    return pNew;
  }

  BinaryTreeNode parent = null;
  BinaryTreeNode pTemp = root;
  while (pTemp != null) {
    parent = pTemp;
    if (d <= pTemp.data) {
      pTemp = pTemp.left;
    } else {
      pTemp = pTemp.right;
    }
  }

  Random generator = new Random();
  int dir = generator.nextInt(1000);

  if (dir%2 == 0) {
    parent.left = pNew;
    pNew.parent = parent;
  } else {
    parent.right = pNew;
    pNew.parent = parent;
  }  
  return root;
}

public static BinaryTreeNode find_in_bst(BinaryTreeNode root, int d){
  if(root == null)
    return null;

  if(root.data == d) {
    return root;
  }
  else if(root.data > d){
    return find_in_bst(root.left,d);
  }
  else{
    return find_in_bst(root.right,d);
  }
}


public static void display_inorder(BinaryTreeNode node) {
  if (node == null) {
    return;
  }
  display_inorder(node.left);
  if(node.parent != null)
  {
    //System.out.print(String.format("[%d - %d]",node.parent.data, node.count));
  }
  System.out.print(node.data + ", ");
  display_inorder(node.right);
}

public static void get_inorder(BinaryTreeNode node, List<Integer> output) {
  if (node == null) {
    return;
  }
  get_inorder(node.left, output);
  output.add(node.data);
  get_inorder(node.right, output);
}

public static void get_preorder(BinaryTreeNode node, List<Integer> output) {
  if (node == null) {
    return;
  }
  output.add(node.data);
  get_preorder(node.left, output);
  get_preorder(node.right, output);
}

public static BinaryTreeNode create_BST(List<Integer> l) {
  BinaryTreeNode root = null;
  for (Integer x : l) {
    root = insert(root, x);
  }
  return root;
}

public static BinaryTreeNode create_random_BST(int count, int max_value) {
  BinaryTreeNode root = null;
  for (int i = 0; i < count; ++i) {
    Random generator = new Random();
    root = insert(root, generator.nextInt(max_value));
  }
  return root;
}

public static BinaryTreeNode create_random_BST(int count) {
  return create_random_BST(count, Integer.MAX_VALUE);
}

public static BinaryTreeNode create_binary_tree(int count) {
  BinaryTreeNode root = null;
  for (int i = 0; i < count; ++i) {
    Random generator = new Random();
    root = insert_BT(root, generator.nextInt(100));
  }
  return root;
}

private static void populate_parents_rec(BinaryTreeNode root, BinaryTreeNode parent) {
  if (root == null) {
    return;
  }

  root.parent = parent;

  populate_parents_rec(root.left, root);
  populate_parents_rec(root.right, root);
}

public static void populate_parents(BinaryTreeNode root) {
  populate_parents_rec(root, null);
}

public static void bst_to_arraylist_rec(BinaryTreeNode root, ArrayList<Integer> arr) {
  if (root == null) {
    return;
  }

  bst_to_arraylist_rec(root.left, arr);
  arr.add(root.data);
  bst_to_arraylist_rec(root.right, arr);
}

public static ArrayList<Integer> bst_to_arraylist(BinaryTreeNode root) {
  ArrayList<Integer> arr = new ArrayList<Integer>();
  bst_to_arraylist_rec(root, arr);
  return arr;
}

public static void another_display_tree(BinaryTreeNode root, int tabs) {
  if (root != null) {
    int i;

    if (root.left != null) {
      for(i = 0; i < tabs+4; ++i) {
        System.out.print(" ");
      }
      System.out.print("L" + root.left.data + "\n");
    }

    if (root.right != null) {
      for(i = 0; i < tabs+4; ++i) {
        System.out.print(" ");
      }
      System.out.print("R" + root.right.data + "\n");
    }

    another_display_tree(root.left, tabs + 4);
    another_display_tree(root.right, tabs + 4);
  }
}

public static void another_display_tree(BinaryTreeNode root) {
  if (root != null) {
    System.out.print(root.data + "\n");
    another_display_tree(root, 0);
  }
}

public static void display_level_order(BinaryTreeNode root) {
  if(root == null)
    return;

  ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<BinaryTreeNode>();
  queue.addLast(root);

  while(!queue.isEmpty()){
    BinaryTreeNode temp = queue.removeFirst();
    System.out.print(temp.data + ", ");

    if(temp.left != null) {
      queue.addLast(temp.left);
      //System.out.println(temp.left.data + "LEFT");
    }

    if(temp.right != null){
      queue.addLast(temp.right);
      //System.out.println(temp.right.data + "RIGHT");
    }
  }
    System.out.println();
}

public static List<Integer> get_level_order(BinaryTreeNode root) {

  List<Integer> output = new ArrayList<Integer>();

  if(root == null)
    return output;

  ArrayDeque<BinaryTreeNode> queue = new ArrayDeque<BinaryTreeNode>();
  queue.addLast(root);

  while(!queue.isEmpty()){
    BinaryTreeNode temp = queue.removeFirst();
    // System.out.print(temp.data + ", ");
    output.add(temp.data);

    if(temp.left != null) {
      queue.addLast(temp.left);
      //System.out.println(temp.left.data + "LEFT");
    }

    if(temp.right != null){
      queue.addLast(temp.right);
      //System.out.println(temp.right.data + "RIGHT");
    }
  }
  return output;
}

public static boolean is_identical_tree(BinaryTreeNode root1, BinaryTreeNode root2) {
  if (root1 == null && root2 == null) {
    return true;
  }
  else if (root1 != null && root2 != null) {
    return ((root1.data == root2.data) &&
            is_identical_tree(root1.left, root2.left) &&
            is_identical_tree(root1.right, root2.right));
  }
  else {
    return false;
  }
}
}

Java

string levelOrderTraversal(BinaryTreeNode* root) {
  string result = "";
  //TODO: Write - Your - Code
  
  return result;
}

#include <iostream>
#include <vector>
#include <queue>
#include <assert.h>
#include <time.h>
#include <math.h>
#include <stack>
#include <cstdlib>
using namespace std;


struct BinaryTreeNode
{
    int data;
    BinaryTreeNode* left;
    BinaryTreeNode* right;
    BinaryTreeNode* parent;

    // below data members used only for some of the problems
    BinaryTreeNode* next;
    int count;

    BinaryTreeNode(int d) : data(d), left(nullptr), right(nullptr), next(nullptr), parent(nullptr), count(0) {
    }
};

BinaryTreeNode* insert_bst(BinaryTreeNode* root, int d) {
  BinaryTreeNode* pNew = new BinaryTreeNode(d);
  if (root == nullptr) {
    return pNew;
  }

  BinaryTreeNode* parent = nullptr;
  BinaryTreeNode* pTemp = root;
  while (pTemp != nullptr) {
    parent = pTemp;
    if (d < pTemp->data) {
      pTemp = pTemp->left;
    } else {
      pTemp = pTemp->right;
    }
  }

  if (d < parent->data) {
    parent->left = pNew;
  } else {
    parent->right = pNew;
  }

  return root;
}

BinaryTreeNode* find_in_bst(BinaryTreeNode* root, int d) {
  if(root == nullptr)
    return nullptr;

  if(root->data == d) {
    return root;
  }
  else if( root->data > d)
  {
    return find_in_bst(root->left, d);
  }
  else
  {
    return find_in_bst(root->right,d);
  }
}

BinaryTreeNode* insert_binary_tree(BinaryTreeNode* root, int d) {
  BinaryTreeNode* pNew = new BinaryTreeNode(d);
  if (root == nullptr) {
    return pNew;
  }

  BinaryTreeNode* parent = nullptr;
  BinaryTreeNode* pTemp = root;
  while (pTemp != nullptr) {
    parent = pTemp;
    if (d < pTemp->data) {
      pTemp = pTemp->left;
    } else {
      pTemp = pTemp->right;
    }
  }

  if (rand()%2 == 0) {
    parent->left = pNew;
  }
  else {
    parent->right = pNew;
  }

  return root;
}

BinaryTreeNode* create_BinaryTree(int count) {
  BinaryTreeNode* root = nullptr;
  for (int i = 0; i < count; ++i) {
    int r = rand() % 100;
    root = insert_binary_tree(root, r);
  }
  return root;
}

void display_inorder(BinaryTreeNode* node) {
  if (node == nullptr) {
    return;
  }
  display_inorder(node->left);
  cout << node->data << ", ";
  display_inorder(node->right);
}

void get_inorder(BinaryTreeNode* node, vector<int>& output) {
  if (node == nullptr) {
    return;
  }
  get_inorder(node->left, output);
  output.push_back(node->data);
  get_inorder(node->right, output);
}

void display_preorder(BinaryTreeNode* node) {
  if (node == nullptr) {
    return;
  }
  cout << node->data << ", ";

  display_preorder(node->left);
  display_preorder(node->right);
}

void get_preorder(BinaryTreeNode* node, vector<int>& output) {
  if (node == nullptr) {
    return;
  }
  output.push_back(node->data);
  get_inorder(node->left, output);
  get_inorder(node->right, output);
}

BinaryTreeNode* create_BST(vector<int>& v) {
  BinaryTreeNode* root = nullptr;
  int count = 0;
  for (int x : v) {
    root = insert_bst(root, x);
    if (count % 50000 == 0) {
      cout << "Inserted " << count << endl;
    }
    ++count;
  }
  return root;
}

BinaryTreeNode* create_random_BST(int count) {
  BinaryTreeNode* root = nullptr;
  srand(time(NULL));
  for (int i = 0; i < count; ++i) {
      int r =  rand() % 997;
      root = insert_bst(root, r);
  }
  return root;
}

void binary_tree_to_vector_rec(BinaryTreeNode* root, vector<int>& v) {
  if (root == nullptr) {
    return;
  }

  binary_tree_to_vector_rec(root->left, v);
  v.push_back(root->data);
  binary_tree_to_vector_rec(root->right, v);
}

vector<int> binary_tree_to_vector(BinaryTreeNode* root) {
  vector<int> v;
  binary_tree_to_vector_rec(root, v);
  return v;
}

string display_BT(BinaryTreeNode* root) {
  string result = "";
  if (root == nullptr) {
    return "";
  }

  queue<BinaryTreeNode*> q;
  q.push(root);
  q.push(nullptr);

  while (!q.empty()) {
    BinaryTreeNode* temp = q.front();
    q.pop();
    result += std::to_string(temp->data) +", ";
    if (temp->left != nullptr) {
      q.push(temp->left);
    }

    if (temp->right != nullptr) {
      q.push(temp->right);
    }

    if (q.front() == nullptr) {
      q.pop();
      if (!q.empty()) {
        q.push(nullptr);
      }
    }

  }
  return result;
}

void get_level_order(BinaryTreeNode* root, vector<int>& output) {
  if (root == nullptr) {
    return;
  }

  queue<BinaryTreeNode*> q;
  q.push(root);

  while (!q.empty()) {
    BinaryTreeNode* temp = q.front();
    q.pop();

    output.push_back(temp->data);
    
    if (temp->left != nullptr) {
      q.push(temp->left);
    }

    if (temp->right != nullptr) {
      q.push(temp->right);
    }
  }
}

void another_display_tree(BinaryTreeNode* root, int tabs) {
  if (root != nullptr) {
    int i;

    if (root->left != nullptr) {
      for(i = 0; i < tabs+4; ++i) {
        cout << ' ';
      }
      cout << "L" << root->left->data << endl;
    }

    if (root->right != nullptr) {
      for(i = 0; i < tabs+4; ++i) {
        cout << ' ';
      }
      cout << "R" << root->right->data << endl;
    }

    another_display_tree(root->left, tabs + 4);
    another_display_tree(root->right, tabs + 4);
  }
}

void another_display_tree(BinaryTreeNode* root) {
  if (root != nullptr) {
    cout << root->data << endl;
    another_display_tree(root, 0);
  }
}

bool is_identical_tree(BinaryTreeNode* root1, BinaryTreeNode* root2) {
  if (root1 == nullptr && root2 == nullptr) {
    return true;
  }
  else if (root1 != nullptr && root2 != nullptr) {
    return ((root1->data == root2->data) &&
            is_identical_tree(root1->left, root2->left) &&
            is_identical_tree(root1->right, root2->right));
  }
  else {
    return false;
  }
}

void populate_parents_rec(BinaryTreeNode* root, BinaryTreeNode* parent) {
  if (root == nullptr) {
    return;
  }

  root->parent = parent;

  populate_parents_rec(root->left, root);
  populate_parents_rec(root->right, root);
}

void populate_parents(BinaryTreeNode* root) {
  populate_parents_rec(root, nullptr);
}

bool are_identical_trees(BinaryTreeNode* root1, BinaryTreeNode* root2) {
  if (root1 == nullptr && root2 == nullptr) {
    return true;
  }
  
  if (root1 != nullptr && root2 != nullptr) {
    return ((root1->data == root2->data) &&
            are_identical_trees(root1->left, root2->left) &&
            are_identical_trees(root1->right, root2->right));
  }

  return false;
}

let levelOrderTraversal = function(root) {
  var result = ""; 
   //TODO: Write - Your - Code
  return result;
};

class TreeNode {
  constructor(data) {
    this.data = data;
    this.children = [];
  }

  display_level_order() {
    if (!this) {
      return;
    }
    let q = [];
    q.push(this);

    while (q.length > 0) {
      let temp = q.shift();
      console.log(temp.data + ",");

      for (let c in temp.children) {
        q.push(temp.children[c]);
      }
    }
  }
}

class BinaryTreeNode {
  constructor(data) {
    this.data = data;
    this.left = null;
    this.right = null;
    this.next = null;
    this.parent = null;
  }
}

class LinkedListNode {
  constructor(data) {
    this.data = data;
    this.next = null;
    this.prev = null;
    this.arbitrary = null;
  }
}

let insert_binary_tree = function(root, d) {
  let pNew = new BinaryTreeNode(d);
  if (!root) {
    return pNew;
  }

  let parent = null;
  let pTemp = root
  while (pTemp) {
    let parent = pTemp;
    if (d < pTemp.data) {
      pTemp = pTemp.left;
    } else {
      pTemp = pTemp.right;
    }
  }
  if (d <= parent.data) {
    parent.right = pNew;
  } else {
    parent.left = pNew;
  }

  return root;
}

let insert = function(root, d) {
  let pNew = new BinaryTreeNode(d);
  if (!root) {
    return pNew;
  }

  let parent = null;
  let pTemp = root;
  while (pTemp) {
    parent = pTemp;
    if (d < pTemp.data) {
      pTemp = pTemp.left;
    } else {
      pTemp = pTemp.right;
    }
  }
  if (d < parent.data) {
    parent.left = pNew;
  } else {
    parent.right = pNew;
  }

  return root;
}

let find_in_bst = function(root, d) {
  if (!root) {
    return null;
  }

  if (root.data === d) {
    return root;
  } else if (root.data > d) {
    return find_in_bst(root.left, d);
  } else {
    return find_in_bst(root.right, d);
  }
}
// find node in inorder 
// works for both BST and binary tree
let find_node = function(root, d) {
  if (!root) {
    return;
  }

  if (root.data === d) {
    return root;
  }

  let temp = find_node(root.left, d);
  if (temp) {
    return temp;
  }

  return find_node(root.right, d);
}

let display_inorder = function(node) {
  if (!node) {
    return;
  }

  display_inorder(node.left);
  console.log(node.data);
  display_inorder(node.right);
}

let create_BST = function(arr) {
  let root = null;
  for (let x in arr) {
    root = insert(root, arr[x]);
  }
  return root;
}

let create_binary_tree = function(count) {
  let root = null;
  for (let i = 1; i < count; i++) {
    root = insert_binary_tree(root, Math.floor(Math.random() * 100 + 1));
  }
  return root;
}

let create_random_BST = function(count) {
  let root = null;
  for (let i = 1; i < count; i++) {
    root = insert(root, Math.floor(Math.random() * 100 + 200));
  }
  return root;
}

let bst_to_list_rec = function(root, lst) {
  if (!root) {
    return;
  }

  bst_to_list_rec(root.left, lst);
  lst.push(root.data);
  bst_to_list_rec(root.right, lst);
}

let bst_to_list = function(root) {
  let lst = [];
  bst_to_list_rec(root, lst);
  return lst;
}

let populate_parents_rec = function(root, parent) {
  if (!root) {
    return;
  }
  root.parent = parent;

  populate_parents_rec(root.left, root);
  populate_parents_rec(root.right, root);
}

let populate_parents = function(root) {
  populate_parents_rec(root, null);
}

let display_level_order = function(root) {
  if (!root) {
    return;
  }
  let q = [];
  q.push(root);
  let print_level = '';
  while (q.length > 0) {
    let temp = q.shift();
    print_level += temp.data + ",";
    if (temp.left) {
      q.push(temp.left);
    }
    if (temp.right) {
      q.push(temp.right)
    }
  }
  console.log(print_level);
}

let get_level_order = function(root) {
  let output = [];
  if (!root) {
    return output;
  }

  let q = [];
  q.push(root);

  while (q.length > 0) {
    let temp = q.shift();
    output.push(temp.data);
    if (temp.left) {
      q.push(temp.left);
    }
    if (temp.right) {
      q.push(temp.right);
    }
  }
  return output;
}

let get_inorder_helper = function(root, output) {
  if (!root) {
    return output;
  }

  output = get_inorder_helper(root.left, output);
  output.push(root.data);
  output = get_inorder_helper(root.right, output);

  return output;
}

let get_inorder = function(root) {
  let output = [];
  return get_inorder_helper(root, output);
}

let is_identical_tree = function(root1, root2) {
  if (!root1 && !root2) {
    return true;
  }

  if (root1 && root2 && root1.data === root2.data) {
    return is_identical_tree(root1.left, root2.left) && is_identical_tree(root1.right, root2.right);
  }

  return false;
}

JavaScript

def level_order_traversal(root)
  result = ""
  #TODO: Write - Your - Code
  return result
end

class BinaryTreeNode
  attr_accessor :data, :left, :right, :next, :parent, :count
  def initialize(data)
    @data = data
    @left = nil
    @right = nil
    @next = nil
    @parent = nil
    @count = -1
  end
end

def insert_binary_tree(root, d)
  pNew = BinaryTreeNode.new(d)
  if (!root)
    return pNew
  end

  parent = nil
  pTemp = root
  while (pTemp)
    parent = pTemp
    if (d < pTemp.data)
      pTemp = pTemp.left
    else
      pTemp = pTemp.right
    end
  end
  if (d <= parent.data)
    parent.right = pNew
  else
    parent.left = pNew
  end

  return root
end

def insert(root, d)
  pNew = BinaryTreeNode.new(d)
  if (!root)
    return pNew
  end

  parent = nil
  pTemp = root
  while (pTemp)
    parent = pTemp
    if (d < pTemp.data)
      pTemp = pTemp.left
    else
      pTemp = pTemp.right
    end
  end
  if (d < parent.data)
    parent.left = pNew
  else
    parent.right = pNew
  end

  return root
end

def find_in_bst(root, d)
  if (!root)
    return nil
  end

  if (root.data == d)
    return root
  elsif (root.data > d)
    return find_in_bst(root.left, d)
  else
    return find_in_bst(root.right, d)
  end
end

# find node in inorder
# works for both BST and binary tree
def find_node(root, d)
  if (!root)
    return
  end

  if (root.data == d)
    return root
  end

  temp = find_node(root.left, d)
  if (temp)
    return temp
  end

  return find_node(root.right, d)
end

def display_inorder(node)
  if (!node)
    return
  end

  display_inorder(node.left)
  print (node.data.to_s + ", ")
  display_inorder(node.right)
end
def create_BST(arr)
  root = nil
  arr.each do |x|
    root = insert(root, x)
  end
  return root
end

def create_binary_tree(count)
  root = nil
  (count-1).times do |i|
    root = insert_binary_tree(root, (rand * 100 + 1).floor)
  end
  return root
end

def create_random_BST(count)
  root = nil
  (count-1).times do |i|
    root = insert(root, (rand * 100 + 200).floor)
  end
  return root
end

def bst_to_list_rec(root, lst)
  if (!root)
    return
  end

  bst_to_list_rec(root.left, lst)
  lst.push(root.data)
  bst_to_list_rec(root.right, lst)
end

def bst_to_list(root)
  lst = []
  bst_to_list_rec(root, lst)
  return lst
end

def populate_parents_rec(root, parent)
  if (!root)
    return
  end
  root.parent = parent

  populate_parents_rec(root.left, root)
  populate_parents_rec(root.right, root)
end

def populate_parents(root)
  populate_parents_rec(root, nil)
end

def display_level_order(root)
  if (!root)
    return
  end
  q = []
  q.push(root)
  print_level = ''
  while (q.length > 0)
    temp = q.shift()
    print_level += temp.data.to_s + ","
    if (temp.left)
      q.push(temp.left)
    end
    if (temp.right)
      q.push(temp.right)
    end
  end
  print (print_level)
end

def get_level_order(root)
  output = []
  if (!root)
    return output
  end

  q = []
  q.push(root)

  while (q.length > 0)
    temp = q.shift()
    output.push(temp.data)
    if (temp.left)
      q.push(temp.left)
    end
    if (temp.right)
      q.push(temp.right)
    end
  end
  return output
end

def get_inorder_helper(root, output)
  if (!root)
    return output
  end

  output = get_inorder_helper(root.left, output)
  output.push(root.data)
  output = get_inorder_helper(root.right, output)

  return output
end

def get_inorder(root)
  output = []
  return get_inorder_helper(root, output)
end

def is_identical_tree(root1, root2)
  if (!root1 && !root2)
    return true
  end

  if (root1 && root2 && root1.data == root2.data)
    return is_identical_tree(root1.left, root2.left) && is_identical_tree(root1.right, root2.right)
  end

  return false
end

Ruby

from collections import deque

def level_order_traversal(root):
    result = []

    if not root:
        result = "None"
        return result

    queue = deque()
    queue.append(root)

    while queue:
        level_size = len(queue)
        level_nodes = []

        for _ in range(level_size):
            temp = queue.popleft()
            level_nodes.append(str(temp.data))

            if temp.left:
                queue.append(temp.left)
            if temp.right:
                queue.append(temp.right)

        result.append(", ".join(level_nodes))

    return "; ".join(result)
  
arr = [100,50,200,25,75,350]
root = create_BST(arr)
print("InOrder Traversal:", end = "")
display_inorder(root)
print("\nLevel Order Traversal: ", level_order_traversal(root))

class levelOrderTraversal{
    
  public static String levelOrderTraversal(BinaryTreeNode root) {
        if (root == null) {
            return "None";
        }

        List<String> result = new ArrayList<>();
        Deque<BinaryTreeNode> queue = new ArrayDeque<>();
        queue.add(root);

        while (!queue.isEmpty()) {
            int levelSize = queue.size();
            List<String> levelNodes = new ArrayList<>();

            for (int i = 0; i < levelSize; i++) {
                BinaryTreeNode temp = queue.poll();
                levelNodes.add(String.valueOf(temp.data));

                if (temp.left != null) {
                    queue.add(temp.left);
                }
                if (temp.right != null) {
                    queue.add(temp.right);
                }
            }

            result.add(String.join(", ", levelNodes));
        }

        return String.join("; ", result);
  }

  public static void main(String[] argv) {

    List<Integer> input = new ArrayList<Integer>();
    input.add(100);input.add(50);input.add(200);input.add(25);input.add(75);input.add(350);
    BinaryTreeNode root = BinaryTree.create_BST(input);
    

    System.out.print("Inorder = ");
    BinaryTree.display_inorder(root);
    System.out.println("\nLevel order = "+ levelOrderTraversal(root));

  }
}  

#include <iostream>
#include <deque>
#include <vector>
#include <string>
#include <sstream>

std::string levelOrderTraversal(BinaryTreeNode* root) {
    if (root == nullptr) {
        return "None";
    }

    std::vector<std::string> result;
    std::deque<BinaryTreeNode*> queue;
    queue.push_back(root);

    while (!queue.empty()) {
        int levelSize = queue.size();
        std::vector<std::string> levelNodes;

        for (int i = 0; i < levelSize; ++i) {
            BinaryTreeNode* temp = queue.front();
            queue.pop_front();
            levelNodes.push_back(std::to_string(temp->data));

            if (temp->left != nullptr) {
                queue.push_back(temp->left);
            }
            if (temp->right != nullptr) {
                queue.push_back(temp->right);
            }
        }

        std::ostringstream oss;
        for (size_t i = 0; i < levelNodes.size(); ++i) {
            if (i != 0) oss << ", ";
            oss << levelNodes[i];
        }
        result.push_back(oss.str());
    }

    std::ostringstream oss;
    for (size_t i = 0; i < result.size(); ++i) {
        if (i != 0) oss << "; ";
        oss << result[i];
    }

    return oss.str();
}

int main(int argc, char* argv[]) {

  BinaryTreeNode* root = create_random_BST(15);
  cout << endl;
  cout << "Inorder = ";
  display_inorder(root);
  cout << "\nLevel order = ";
  cout<< levelOrderTraversal(root);
  
}

def level_order_traversal(root)
  return "None" if root.nil?

  result = []
  queue = []
  queue.push(root)

  until queue.empty?
    level_size = queue.size
    level_nodes = []

    level_size.times do
      temp = queue.shift
      level_nodes.push(temp.data.to_s)

      queue.push(temp.left) if temp.left
      queue.push(temp.right) if temp.right
    end

    result.push(level_nodes.join(", "))
  end

  result.join("; ")
end

def main()
  arr = [100,50,200,25,75,350]
  root = create_BST(arr)
  print "\nIn Order Traversal: "
  display_inorder(root)
  #display_level_order(root)
  print "\nLevel Order Traversal1: "
  print level_order_traversal(root)
end

main()

## Solution Explanation
### Runtime Complexity
The runtime complexity of this solution is linear, $O(n)$.

### Memory Complexity 
The memory complexity of this solution is linear, $O(n)$.

<br>

### Solution Breakdown
1. Initialize a queue, `queue`, with the root node.

2. Iterate over the `queue` until it’s empty:
   - For each level, calculate the size `(level_size)` of the queue.
   - Initialize an empty list `level_nodes`.
   - Iterate `level_size` times:
      - Dequeue a node from the `queue`.
      - Append the value of the dequeued node in `level_nodes`.
      - Enqueue the left child and the right child of the dequeued node in `queue`, if they exist.
   - Convert `level_nodes` to a comma-separated string and store it in `result`.
3. Return the `result`.

> Practice problems like this and many more by checking out our [Grokking the Coding Interview: Patterns for Coding Questions](https://www.educative.io/courses/grokking-the-coding-interview) course!

Given the root of a binary tree, display the node values at each level.

Level Order Traversal of Binary Tree

Problem Statement

Hint

Try it yourself

Solution

Solution Explanation

Runtime Complexity

Memory Complexity

Solution Breakdown