Merge Overlapping Intervals

Problem Statement

You are given an array (list) of interval pairs as input where each interval has a start and end timestamp. The input array is sorted by starting timestamps. You are required to merge overlapping intervals and return a new output array.

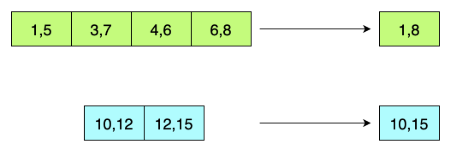
Consider the input array below. Intervals (1, 5), (3, 7), (4, 6), (6, 8) are overlapping so they should be merged to one big interval (1, 8). Similarly, intervals (10, 12) and (12, 15) are also overlapping and should be merged to (10, 15).

class Pair{
  public:
    int first, second;
    Pair(int x, int y){
      first = x;
      second = y; 
    }
};
vector<Pair> merge_intervals(vector<Pair>& v) {
  if(v.size() == 0) {
    return v;
  }
  vector<Pair> result;
  result.push_back(Pair(v[0].first, v[0].second));
  for(int i = 1 ; i < v.size(); i++){
    int x1 = v[i].first;
    int y1 = v[i].second;
    int x2 = result[result.size() - 1].first;
    int y2 = result[result.size() - 1].second;
    if(y2 >= x1){
      result[result.size() - 1].second = max(y1, y2);
    }
    else{
      result.push_back(Pair(x1, y1));
    }
  }
  return result;
}
int main() {
  vector<Pair> v {
                  Pair(1, 5),
                  Pair(3, 7),
                  Pair(4, 6),
                  Pair(6, 8),
                  Pair(10, 12),
                  Pair(11, 15)
                  };
  vector<Pair> result = merge_intervals(v);
  
  for(int i = 0; i < result.size(); i++){
    cout << "[" << result[i].first << ", " << result[i].second << "] ";
  }
}

Solution Explanation

Runtime complexity

The runtime complexity of this solution is linear, O(n).

Memory complexity

The memory complexity of this solution is linear, O(n).

Solution Breakdown

This problem can be solved in a simple linear scan algorithm. We know that input is sorted by starting timestamps. Here is the approach we are following:

List of input intervals is given, and we’ll keep merged intervals in the output list.
For each interval in the input list:
- If the input interval is overlapping with the last interval in output list then we’ll merge these two intervals and update the last interval of output list with merged interval.
- Otherwise, we’ll add an input interval to the output list.

Merge Overlapping Intervals

Problem Statement

Hint

Try it yourself

Solution

Solution Explanation

Runtime complexity

Memory complexity

Solution Breakdown