Regular Expression
Problem Statement
Given a text and a pattern, determine if the pattern matches with the text completely or not at all by using regular expression matching. For simplicity, assume that the pattern may contain only two operators: ‘.’ and ‘’. Operator '’ in the pattern means that the character preceding ‘*’ may not appear or may appear any number of times in the text. Operator ‘.’ matches with any character in the text exactly once.
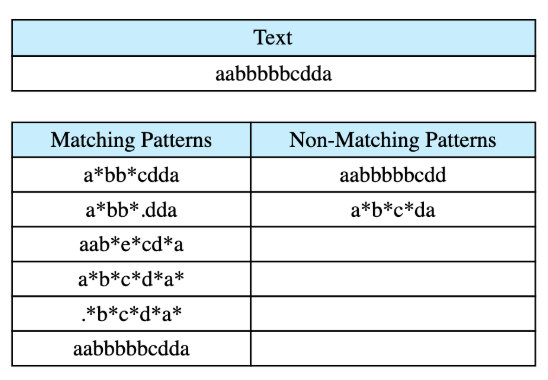
Below is an example of a text and its matching and non-matching patterns.
Hint
- Recursion
Try it yourself
bool regx_match(const string& text, const string& pattern) {//TODO: Write - Your - Codereturn false;}
Solution
bool regx_match_rec(const string & text,const string & pattern,int i, int j) {if (pattern.length() == j) {if (text.length() == i) {return true;} else {return false;}}if (j < pattern.length() - 1 && pattern[j + 1] == '*') {for (int k = i; k <= text.length(); ++k) {if (regx_match_rec(text, pattern, k, j + 2)) {return true;}if (pattern[j] != '.' && text[k] != pattern[j]) {return false;}}} else if (i < text.length() && j < pattern.length() &&(pattern[j] == '.' || pattern[j] == text[i])) {return regx_match_rec(text, pattern, i + 1, j + 1);}return false;}bool regx_match(const string & text, const string & pattern) {return regx_match_rec(text, pattern, 0, 0);}int main() {string text = "fabbbc";string pattern = ".ab*c";bool match1 = regx_match(text, pattern);cout << text << " " << pattern;cout << (match1 ? " match" : " did not match.");smatch m;regex e(pattern);bool expected = regex_match(text, m, e);assert(match1 == expected);cout << endl;}
Solution Explanation
Runtime complexity
The runtime complexity of this solution is exponential,
Memory complexity
The memory complexity of this solution is exponential,
Solution Breakdown
We’ll compare the text and pattern character by character and recursively compare the remaining text and remaining pattern. In this solution, we use indices of text and pattern instead of creating sub-strings and pass the same strings in the recursive calls.
The worst-case time complexity for this solution is still exponential, but we do save memory and time that was previously being spent on copying strings. For example, if text is aaa and pattern is aaa*. First, we’ll match aa with aaa, aa, a, and an empty string. Then we’ll match a* with aaa, aa, a, and an empty string.
Practice problems like this and many more by checking out our Grokking the Coding Interview: Patterns for Coding Questions course!