Serialize/Deserialize Binary Tree
Problem Statement
Serialize a binary tree to a file and then deserialize it back to a tree so that the original and the deserialized trees are identical.
Serialize: write the tree in a file.
Deserialize: read from a file and reconstruct the tree in memory.
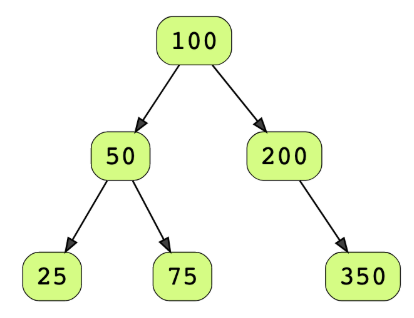
Consider the below tree as the input tree.
There is no restriction regarding the format of a serialized stream, therefore you can serialize it in any efficient format. However, after deserializing the tree from the stream, it should be exactly like the original tree.
Hint
- Depth first traversal
Try it yourself
void serialize(BinaryTreeNode* node, ostream& sstream) {//TODO: Write - Your - Code}BinaryTreeNode* deserialize(istream& sstream) {//TODO: Write - Your - Code}
Solution
const int MARKER = numeric_limits<int>::min();void serialize(BinaryTreeNode* node, ostream& sstream) {if (node == nullptr) {sstream.write((char*) &MARKER, sizeof(MARKER));return;}sstream.write((char*) &node->data, sizeof(node->data));serialize(node->left, sstream);serialize(node->right, sstream);}BinaryTreeNode* deserialize(istream& sstream) {if (sstream.eof()) {return nullptr;}int val;sstream.read((char*) &val, sizeof(val));if (val == MARKER) {return nullptr;}BinaryTreeNode* pNode = new BinaryTreeNode(val);pNode->left = deserialize(sstream);pNode->right = deserialize(sstream);return pNode;}void test(vector<int>& v, bool display_output = false) {cout << "Create BST" << endl;BinaryTreeNode* root = create_BST(v);if (display_output) {display_preorder(root);}cout << "Start Serialize" << endl;ofstream outfile("temp.class", ios::binary);serialize(root, outfile);outfile.close();cout << "Start De-Serialize" << endl;ifstream infile("temp.class", ios::binary);BinaryTreeNode* root2 = deserialize(infile);infile.close();if (display_output) {cout << "\nAfter:\n";display_preorder(root2);cout << endl << endl;}assert(are_identical_trees(root, root2));}int main(int argc, char const *argv[]) {vector<int> v = { 50, 25, 100 };test(v, true);v = {10 , 3, 8, 45, 9, 35, 69, 15, 12, 25, 24, 27, 13};test(v, true);v = create_random_vector(100);test(v, true);v = create_random_vector(2000000,numeric_limits<int>::max() - 10);cout << "\nRun big test" << endl;test(v, false);return 0;}
Solution Explanation
Runtime Complexity
Linear, O(n).
Memory Complexity
Logarithmic, O(logn).
Recursive solution has O(h) memory complexity as it will consume memory on the stack up to the height of the binary tree h. It will be O(logn) for a balanced tree and in the worst case can be O(n).
Solution Breakdown
There can be multiple approaches to serialize and deserialize the tree. One approach is to perform a depth-first traversal and serialize individual nodes to the stream. We’ll use a pre-order traversal here. We’ll also serialize some marker to represent a null pointer to help deserialize the tree.
Consider the below binary tree as an example. Markers (M*) have been added in this tree to represent null nodes. The number with each marker i.e. 1 in M1, 2 in M2, merely represents the relative position of a marker in the stream.
The serialized tree (pre-order traversal) from the above example would look like the below list.
When deserializing the tree we’ll again use the pre-order traversal and create a new node for every non-marker node. Encountering a marker indicates that it was a null node.
Practice problems like this and many more by checking out our Grokking the Coding Interview: Patterns for Coding Questions course!