## Problem Statement
Given an array of integers and a value, determine if there are any three integers in the array whose sum equals the given value.

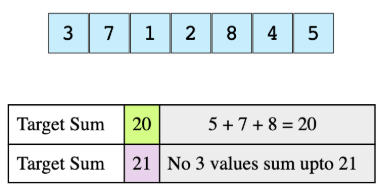
Consider this array and the target sums.

<br>

## Hint
* Sort data
* Iterate from both ends

<br>

## Try it yourself

bool find_sum_of_three(vector<int> arr,
  int required_sum) {
  // TODO: Write - Your - Code

  return false;
}

#include <string>
#include <list>
#include <iostream>
#include <vector>
#include <algorithm>
#include <unordered_map>
using namespace std;

class sumOfThree{
  public static Boolean
  find_sum_of_three(int arr[], int required_sum) {
     // TODO: Write - Your - Code

    return false;
  }
} 

Java

def find_sum_of_three(arr, required_sum):
  # TODO: Write - Your - Code
  return False

import os, sys
from bisect import bisect_left
utils_path = os.path.join('..', '..', '..', '..', 'problems', 'utils', 'python')
sys.path.append(utils_path)

import random
def create_random_int_array(length):
  arr = []
  for i in range(0, length):
    arr.append(random.randrange(1, 1000))
  return arr

def print_list(arr):
  for i in range(0, len(arr)):
    print(str(arr[i]), end = ",")
  print()

def is_equal(arr1, arr2):
  if len(arr1) != len(arr2):
    return False

  for i in range(0, len(arr1)):
    if arr1[i] != arr2[i]:
      return False

  return True

class pair:
  def __init__(self, first, second):
    self.first = first
    self.second = second
     
def print_incides(arr, sum, i, j, k):
  print("Sum: {}, Indices: {}, {}, {}, Values: {}, {}, {}"\
    .format(sum, i,j,k, arr[i], arr[j], arr[k]))

Python

let find_sum_of_three = function(arr, required_sum) {
  // TODO: Write - Your - Code
 return false;
};

JavaScript

def find_sum_of_three(arr, required_sum)
  # TODO: Write - Your - Code
  return false
end

Ruby

bool find_sum_of_two(vector<int>& A, int val,
  size_t start_index) {
  for (int i = start_index, j = A.size() - 1; i < j;) {
    int sum = A[i] + A[j];
    if (sum == val) {
      return true;
    }

    if (sum < val) {
      ++i;
    } else {
      --j;
    }
  }

  return false;
}

bool find_sum_of_three_v3(vector<int> arr,
  int required_sum) {

  std::sort(arr.begin(), arr.end());

  for (int i = 0; i < arr.size() - 2; ++i) {
    int remaining_sum = required_sum - arr[i];
    if (find_sum_of_two(arr, remaining_sum, i + 1)) {
      return true;
    }
  }

  return false;
}

int main(){
    vector<int> arr = {-25, -10, -7, -3, 2, 4, 8, 10};
  
    cout<<"-8: " <<find_sum_of_three_v3(arr, -8)<<endl; 
    cout<<"-25: "<<find_sum_of_three_v3(arr, -25)<<endl;
    cout<<"0: " <<find_sum_of_three_v3(arr, 0)<<endl;
    cout<<"-42: " <<find_sum_of_three_v3(arr, -42)<<endl; 
    cout<<"22: " <<find_sum_of_three_v3(arr, 22)<<endl; 
    cout<<"-7: " <<find_sum_of_three_v3(arr, -7)<<endl;
    cout<<"-3: " <<find_sum_of_three_v3(arr, -3)<<endl; 
    cout<<"2: " <<find_sum_of_three_v3(arr, 2)<<endl; 
    cout<<"4: " <<find_sum_of_three_v3(arr, 4)<<endl; 
    cout<<"8: " <<find_sum_of_three_v3(arr, 8)<<endl; 
    cout<<"7: " <<find_sum_of_three_v3(arr, 7)<<endl; 
    cout<<"1: " <<find_sum_of_three_v3(arr, 1)<<endl;
  
    return 0;
}

class sumOfThree{
  static boolean find_sum_of_two(int[] A, int val, int start_index) {

    for (int i = start_index, j = A.length - 1; i < j;) {
      int sum = A[i] + A[j];
      if (sum == val) {
        return true;
      }  

      if (sum < val) {
        ++i;
      } else {
        --j;
      }
    }

    return false;
  }

  public static Boolean
  find_sum_of_three_v3(int arr[], int required_sum) {
    Arrays.sort(arr);
    for (int i = 0; i < arr.length-2; ++i) {
      int remaining_sum = required_sum - arr[i];
      if (find_sum_of_two(arr, remaining_sum, i + 1)) {
        return true;
      }
    }  
    return false;
  }
  public static void main(String []args){
    int[] arr = {-25, -10, -7, -3, 2, 4, 8, 10};
    System.out.println("-8: " +find_sum_of_three_v3(arr, -8)); 
    System.out.println("-25: " +find_sum_of_three_v3(arr, -25));
    System.out.println("0: " +find_sum_of_three_v3(arr, 0));
    System.out.println("-42: " +find_sum_of_three_v3(arr, -42)); 
    System.out.println("22: " +find_sum_of_three_v3(arr, 22)); 
    System.out.println("-7: " +find_sum_of_three_v3(arr, -7));
    System.out.println("-3: " +find_sum_of_three_v3(arr, -3)); 
    System.out.println("2: " +find_sum_of_three_v3(arr, 2)); 
    System.out.println("4: " +find_sum_of_three_v3(arr, 4)); 
    System.out.println("8: " +find_sum_of_three_v3(arr, 8)); 
    System.out.println("7: " +find_sum_of_three_v3(arr, 7)); 
    System.out.println("1: " +find_sum_of_three_v3(arr, 1));  
  }
} 

def find_sum_of_two(A, val, start_index):
  i = start_index
  j = len(A) - 1
  while i < j:
    s = A[i] + A[j]
    if s == val:
      return True

    if s < val:
      i += 1
    else:
      j -= 1

  return False

def find_sum_of_three_v3(arr, required_sum):
  arr.sort()
  for i in range(0, len(arr)-2):
    remaining_sum = required_sum - arr[i]
    if find_sum_of_two(arr, remaining_sum, i+1):
      return True

  return False

def test():
  arr = [-25, -10, -7, -3, 2, 4, 8, 10]
  print(find_sum_of_three_v3(arr, -8)) 
  print(find_sum_of_three_v3(arr, -25))
  print(find_sum_of_three_v3(arr, 0))
  print(find_sum_of_three_v3(arr, -42))
  print(find_sum_of_three_v3(arr, 22))
  print(find_sum_of_three_v3(arr, -7))
  print(find_sum_of_three_v3(arr, -3)) 
  print(find_sum_of_three_v3(arr, 2)) 
  print(find_sum_of_three_v3(arr, 4)) 
  print(find_sum_of_three_v3(arr, 8))
  print(find_sum_of_three_v3(arr, 7)) 
  print(find_sum_of_three_v3(arr, 1))
  
test()

def find_sum_of_two_sol(arr, val, start_index)
  i = start_index
  j = arr.length - 1
  while (i < j)
    sum = arr[i] + arr[j]
    if (sum == val)
      return true
    end

    if (sum < val)
      i+=1
    else
      j-=1
    end
  end
  return false
end

def find_sum_of_three_v3(arr, required_sum)
  arr.sort!

  for i in 0 .. arr.length-3
    remaining_sum = required_sum - arr[i]
    if (find_sum_of_two_sol(arr, remaining_sum, i + 1))
      return true
    end
  end
  return false
end

def test()
  arr = [-25, -10, -7, -3, 2, 4, 8, 10]
  puts find_sum_of_three_v3(arr, -8) 
  puts find_sum_of_three_v3(arr, -25)
  puts find_sum_of_three_v3(arr, 0)
  puts find_sum_of_three_v3(arr, -42) 
  puts find_sum_of_three_v3(arr, 22) 
  puts find_sum_of_three_v3(arr, -7)
  puts find_sum_of_three_v3(arr, -3) 
  puts find_sum_of_three_v3(arr, 2) 
  puts find_sum_of_three_v3(arr, 4) 
  puts find_sum_of_three_v3(arr, 8) 
  puts find_sum_of_three_v3(arr, 7) 
  puts find_sum_of_three_v3(arr, 1)
end

test

## Solution Explanation
### Runtime Complexity
Quadratic, O(n2)

### Memory Complexity
Constant, O(1)

<br>

### Solution Breakdown

In this solution, we first sort the array. Then we fix one element 'e', and try to find a pair (a, b) in the remaining array such that required_sum - e = a + b.

We start with the first element e in the array (at index i = 0) and try to find such a pair (a, b) in the remaining array (i.e A[i + 1] to A[n - 1]) that satisfies the condition: a+b = required_sum - e. We can find such a pair in linear time. If we find such a pair, we have found the solution: a, b and e and thus, we can stop the iteration.

Otherwise, we repeat the above steps for all elements e at index i = 1 to n - 3, until we find a pair that meets the condition.

> Practice problems like this and many more by checking out our [Grokking the Coding Interview: Patterns for Coding Questions](https://www.educative.io/courses/grokking-the-coding-interview) course!

Given an array of integers and a value, determine if there are any three integers in the array whose sum equals the given value.

Sum of Three Values

Problem Statement

Hint

Try it yourself

Solution

Solution Explanation

Runtime Complexity

Memory Complexity

Solution Breakdown