Data structures 101: A deep dive into trees with Java

Data structures are an important part of programming and coding interviews. These skills show your ability to think complexly, solve ambiguous problems, and recognize coding patterns.

Programmers use data structures to organize data, so the more efficient your data structures are, the better your programs will be.

Today, we will take a deep dive into one of the most popular data structures out there: trees.

Today, we will cover:

• What is a tree?
• Types of trees
• Intro to tree traversal and searching
• Next steps and wrapping up

Components of a Tree#

Trees are a collection of nodes (vertices), and they are linked with edges (pointers), representing the hierarchical connections between the nodes. A node contains data of any type, but all the nodes must be of the same data type. Trees are similar to graphs, but a cycle cannot exist in a tree. What are the different components of a tree?

Root: The root of a tree is a node that has no incoming link (i.e. no parent node). Think of this as a starting point of your tree.

Children: The child of a tree is a node with one incoming link from a node above it (i.e. a parent node). If two children nodes share the same parent, they are called siblings.

Parent: The parent node has an outgoing link connecting it to one or more child nodes.

Leaf: A leaf has a parent node but has no outgoing link to a child node. Think of this as an endpoint of your tree.

Subtree: A subtree is a smaller tree held within a larger tree. The root of that tree can be any node from the bigger tree.

Depth: The depth of a node is the number of edges between that node and the root. Think of this as how many steps there are between your node and the tree’s starting point.

Height: The height of a node is the number of edges in the longest path from a node to a leaf node. Think of this as how many steps there are between your node and the tree’s endpoint. The height of a tree is the height of its root node.

Degree: The degree of a node refers to the number of sub-trees.

Why do we use trees?#

Trees can be applied to many things. The hierarchical structure gives a tree unique properties for storing, manipulating, and accessing data. Trees form some of the most basic organization of computers. We can use a tree for the following:

• Storage as hierarchy. Storing information that naturally occurs in a hierarchy. File systems on a computer and PDF use tree structures.
• Searching. Storing information that we want to search quickly. Trees are easier to search than a Linked List. Some types of trees (like AVL and Red-Black trees) are designed for fast searching.
• Inheritance. Trees are used for inheritance, XML parser, machine learning, and DNS, amongst many other things.
• Indexing. Advanced types of trees, like B-Trees and B+ Trees, can be used for indexing a database.
• Networking. Trees are ideal for things like social networking and computer chess games.
• Shortest path. A Spanning Tree can be used to find the shortest paths in routers for networking.
• and much more

How to make a tree#

But, how does that all look in code? To build a tree in Java, for example, we start with the root node.

Node<String> root = new Node<>("root");

Once we have our root, we can add our first child node using addChild, which adds a child node and assigns it to a parent node. We refer to this process as insertion (adding nodes) and deletion (removing nodes).

Node<String> node1 = root.addChild(new Node<String>("node 1"));

We continue adding nodes using that same process until we have a complex hierarchical structure. In the next section, let’s look at the different kinds of trees we can use.

Note: The balance factor of a node is the height difference between the left and right subtrees.

Balanced Tree#

A balanced tree is a tree with almost all leaf nodes at the same level, and it is most commonly applied to sub-trees, meaning that all sub-trees must be balanced. In other words, we must make the tree height balanced, where the difference between the height of the right and left subtrees do not exceed one. Here is a visual representation of a balanced tree.

There are three main types of binary trees based on their structures.

1. Complete Binary Tree#

A complete binary tree exists when every level, excluding the last, is filled and all nodes at the last level are as far left as they can be. Here is a visual representation of a complete binary tree.

2. Full Binary Tree#

A full binary tree (sometimes called proper binary tree) exits when every node, excluding the leaves, has two children. Every level must be filled, and the nodes are as far left as possible. Look at this diagram to understand how a full binary tree looks.

3. Perfect Binary Tree#

A perfect binary tree should be both full and complete. All interior nodes should have two children, and all leaves must have the same depth. Look at this diagram to understand how a perfect binary tree looks.

Note: You can also have a skewed binary tree, where all the nodes are shifted to the left or right, but it is best practice to avoid this type of tree in Java, as it is far more complex to search for a node.

Binary Search Trees#

A Binary Search Tree is a binary tree in which every node has a key and an associated value. This allows for quick lookup and edits (additions or removals), hence the name “search”. A Binary Search Tree has strict conditions based on its node value. It’s important to note that every Binary Search Tree is a binary tree, but not every binary tree is a Binary Search Tree.

What makes them different? In a Binary Search Tree, the left subtree of a subtree must contain nodes with fewer keys than a node’s key, while the right subtree will contain nodes with keys greater than that node’s key. Take a look at this visual to understand this condition.

In this example, the node Y is a parent node with two child nodes. All nodes in subtree 1 must have a value less than node Y, and subtree 2 must have a greater value than node Y.

AVL Trees#

AVL trees are a special type of Binary Search tree that are self-balanced by checking the balance factor of every node. The balance factor should either be +1, 0, or -1. The maximum height difference between the left and right sub-trees can only be one.

If this difference becomes more than one, we must re-balance our tree to make it valid using rotation techniques. These are most common for applications where searching is the most important operation. Look at this visual to see a valid AVL tree.

Red-Black Trees#

A red-black tree is another type of self-balancing Binary Search Tree, but it has some additional properties to AVL trees. The nodes are colored either red or black to help re-balance a tree after insertion or deletion. They save you time with balancing. So, how do we color our nodes?

• The root is always black
• Two red nodes cannot be adjacent (i.e. a red parent cannot have a red child)
• A path from the root to a leaf should contain the same number of black nodes
• A null node is black

2-3 Trees#

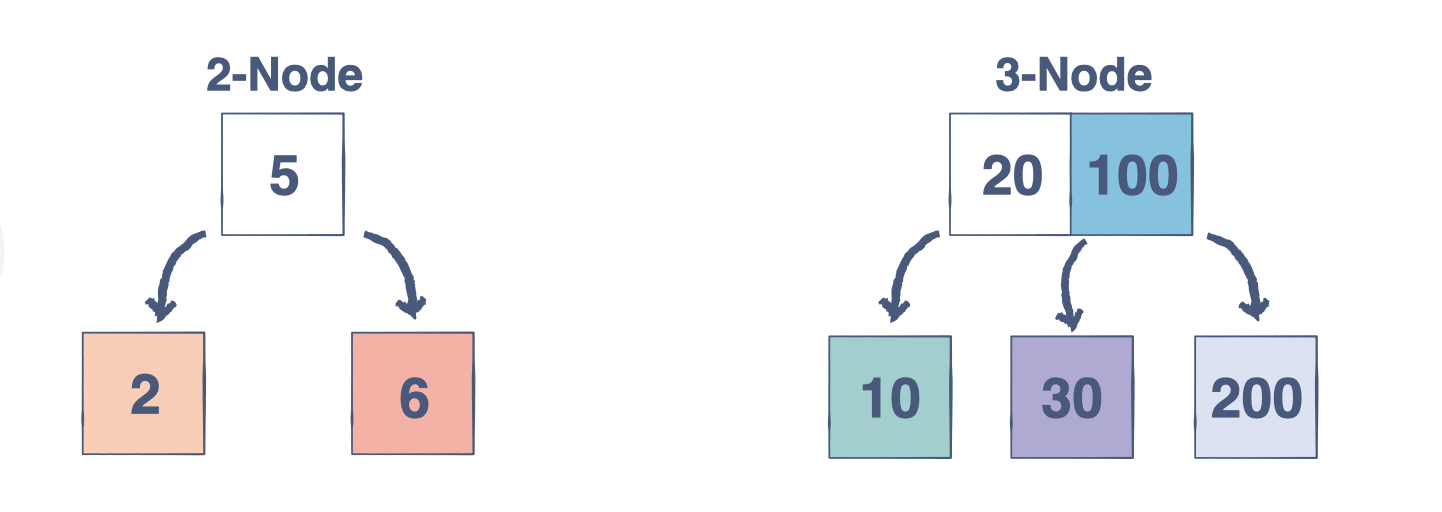
A 2-3 tree is very different from what we’ve learned so far. Unlike a Binary Search Tree, a 2-3 Tree is a self-balancing, ordered, multiway search tree. It is always perfectly balanced, so every leaf node is equidistant from the root. Every node, other than leaf nodes, can be either a 2-Node (a node with a single data element and two children) or a 3-node (a node with two data elements and three children). A 2-3 tree will remain balanced no matter how many insertions or deletions occur.

2-3-4 Trees#

A 2-3-4 tree is a search tree that can accommodate more keys than a 2-3 tree. It covers the same basics as a 2-3 tree, but adds the following properties:

• 2-Node has two child nodes and one data element
• 3-Node has three child nodes and two data elements
• 4-Node has four child nodes and three data elements
• Each internal node has a max of 4 children
• For three keys at an internal node, all keys at the LeftChild node are smaller than the left key
• All keys at the LeftMidChild are smaller than the mid key
• All keys at the RightMidChild are smaller than the right key
• All keys at the RightChild are greater than the right key

Depth-First Search#

Overview: We follow a path from the starting node to the ending node and then start another path until all nodes are visited. This is commonly implemented using stacks, and it requires less memory than BFS. It is best for topographical sorting, such as graph backtracking or cycle detection.

The steps for the DFS algorithm are as follows:

1. Pick a node. Push all adjacent nodes into a stack.
2. Pop a node from that stack and push adjacent nodes into another stack.
3. Repeat until the stack is empty or you have reached your goal. As you visit nodes, you must mark them as visited before proceeding, or you will be stuck in an infinite loop.

Breadth-First Search#

Overview: We proceed level-by-level to visit all nodes at one level before going to the next. The BFS algorithm is commonly implemented using queues, and it requires more memory than the DFS algorithm. It is best for finding the shortest path between two nodes.

The steps for the BFS algorithm are as follows:

1. Pick a node. Enqueue all adjacent nodes into a queue. Dequeue a node, and mark it as visited. Enqueue all adjacent nodes into another queue.
2. Repeat until the queue is empty of you have met your goal.
3. As you visit nodes, you must mark them as visited before proceeding, or you will be stuck in an infinite loop.

Search in Binary Search Trees#

It’s important to know how to perfom a search in a tree. Searching means we are locating a specific element or node in our data structure. Since data in a Binary Search Tree is ordered, searching is quite easy. Let’s see how it’s done.

1. Start at the root.
2. If the value is less than the value of the current node, we traverse the left sub-tree. If it is more, we traverse the right sub-tree.
3. Continue this process until you reach a node with that value or reach a leaf node, meaning that the value doesn’t exist.

In the below example, we are searching for the value 3 in our tree. Take a look.

Let’s see that in Java code now!