Algorithms 101: how to implement Tree Traversal in JavaScript
Understanding algorithms is important for every software developer to have. Algorithms are a common part of any coding interview, whether you are solving problems in JavaScript, Java, or Python. You can utilize algorithms to ace coding interviews, land a job, or solve peculiar problems at work.
Today’s tutorial would focus on algorithms for traversing elements in a tree. Tree traversal looks different in different programming languages; we will be using JavaScript. We start by refreshing our knowledge about trees. Next, we will learn some useful algorithms and look at some common interview questions.
This guide at a glance:
Get hands-on interview practice in JavaScript
In this curated learning path, you’ll cover everything from Data Structures to System Design.
Ace the JavaScript Coding Interview
What are trees?#
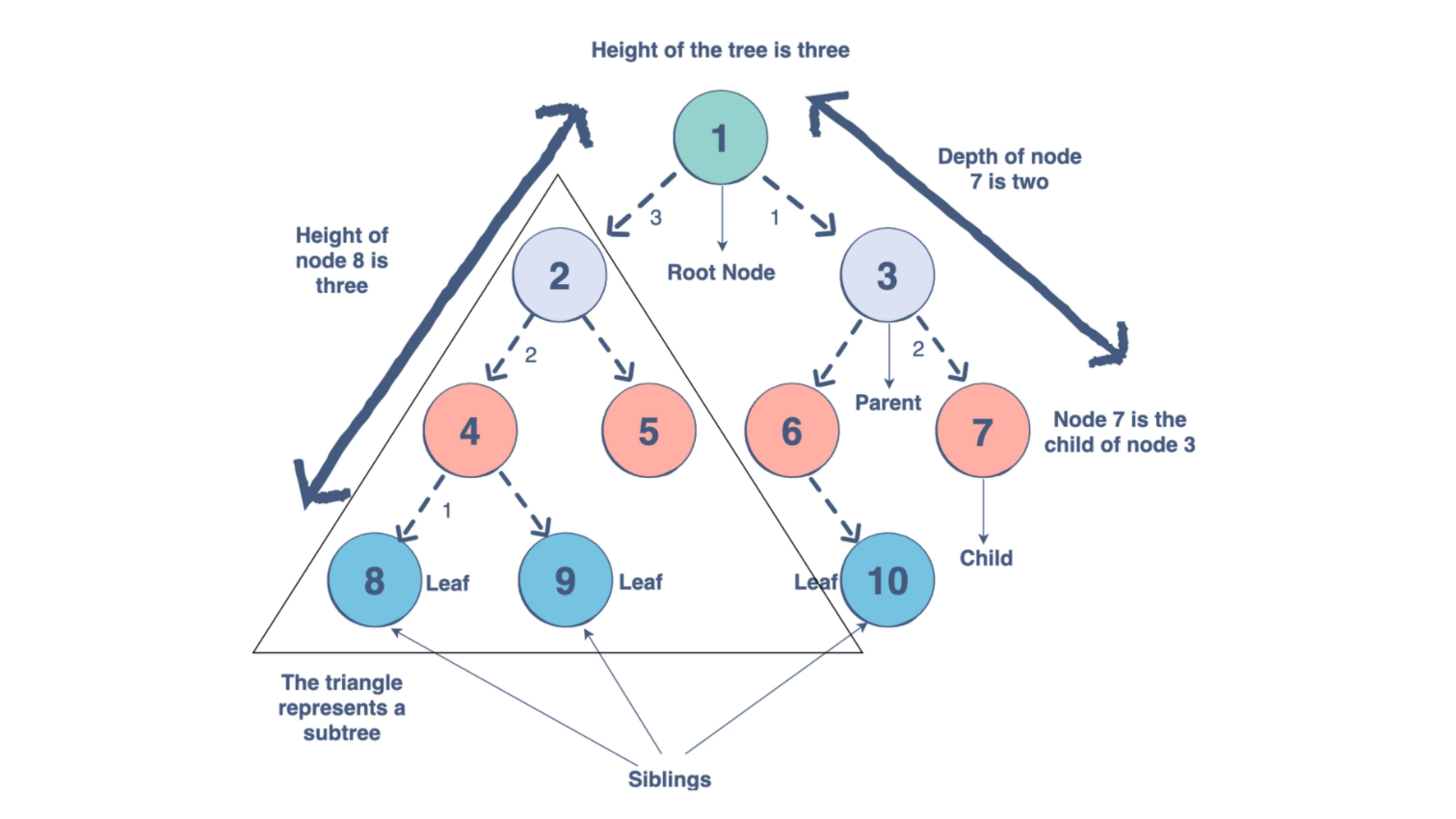
In computer science, trees are non-linear data structures represented as a collection of nodes connected by edges. Each node stores data of any type, and all nodes in a tree are the same data type.
Tree data structures are typically used to store information while preserving its hierarchy, for implementing quick searches, networking, and inheritance.
The basic components of a tree includes:
- The root, which is the top-most node (it has no parent node). This is typically the starting point of your tree.
- The parent node, which is connected downwards to one or two nodes.
- The child node, which has an incoming link (or connecting edge) from a parent node above it.
- Sibling nodes are nodes that share the same parent.
- The leaf nodes have parent nodes but no children nodes. They are typically the base/bottom nodes.
- A subtree is a tree held within a larger tree.
- The degree of a node refers to the number of subtrees within a tree.
- The depth of a tree refers to the number of edges between a specific node and the root.
- The height of a node refers to the number of edges in the longest path from a specified node to a leaf node.
How to traverse trees#
A traversed tree is one in which every node on the tree has been visited. Traversal is a process involving iterating over all nodes in a certain manner.
Unlike linear data structures (such as Arrays, Linked Lists, or Queues) which have only one logical way to traverse them with recursion, trees can be traversed in different ways. Generally there are 2 iterative ways for traversing trees:
- Depth-first Search/Traversal (DFS)
- Breadth-first Search/Traversal (BFS)
Depth-first Traversal#
Depth-first traversal involves traversing a tree from top to bottom. They are implemented in a FILO manner (First In Last Out), like the stack data structure. The left sub-trees are traversed first, then the right sub-trees.
This is commonly seen when traversing a binary tree. Binary Trees are trees where each node has at most 2 child nodes. In the tree below, the node with the value 1 would be the first to be pushed into a stack, followed by the nodes with values 2, 3, and 4, then it goes back to the top to the node with the value 5 down.
When the end of the tree is reached, the values are popped off the stack back into the tree.
There are 3 types of Depth-first traversal:
1. In-Order Traversal#
In in-order traversal, we traverse the left child and its sub-tree(s), then we visit the root and then traverse the right child and its sub-tree(s). It takes a “left-root-right” order.
Before we take a look at a code sample for this algorithm, let’s try to outline the steps involved:
- Starting at the root node, we traverse the left node and its sub-trees recursively
- We start reading from the left leaf node, followed by its parent and sibling node
- We do this recursively until we get back to the root node, then we repeat the process for the right node, starting our reading from its leftmost leaf node
inOrderprint(currentNode) {//if the currentNode IS NOT EQUAL to nullif (currentNode!==null) {//make recursive call to the left subtreethis.inOrderPrint(currentNode.leftChild);//print the value of the currentNodeconsole.log(currentNode.val);//make recursive call to the right subtreethis.inOrderPrint(currentNode.rightChild);}}
class Node {constructor(value) {this.val = value;this.leftChild = null;this.rightChild = null;}}class BinarySearchTree {constructor(rootValue) {this.root = new Node(rootValue);}insert(currentNode, newValue) {if (currentNode === null) {currentNode = new Node(newValue);} else if (newValue < currentNode.val) {currentNode.leftChild = this.insert(currentNode.leftChild, newValue);} else {currentNode.rightChild = this.insert(currentNode.rightChild, newValue);}return currentNode;}insertBST(newValue) {if(this.root==null){this.root=new Node(newValue);return;}this.insert(this.root, newValue);}preOrderPrint(currentNode) {if (currentNode!==null) {console.log(currentNode.val);this.preOrderPrint(currentNode.leftChild);this.preOrderPrint(currentNode.rightChild);}}inOrderPrint(currentNode) {if (currentNode!==null) {this.inOrderPrint(currentNode.leftChild);console.log(currentNode.val);this.inOrderPrint(currentNode.rightChild);}}}var BST = new BinarySearchTree(6);console.log("The root val for BST : ", BST.root.val)BST.insertBST(4);BST.insertBST(9);BST.insertBST(5);BST.insertBST(2);BST.insertBST(8);BST.insertBST(12);BST.inOrderPrint(BST.root);
In our implementation, we create an object named BST of the BinarySearchTree class and insert some values into it. We will then pass the object’s root to the inOrderPrint() function as a starting point to the traversal.
If the node passed into the function is not null, this function calls inOrderPrint() recursively on the left child first, i.e., the left subtree, and then prints the value at the node. Then it calls the inOrderPrint() recursively on the right child, i.e., the right subtree.
The node will print its own value once all the subsequent calls to the left subtree have been executed.
When the recursive calls will hit the null nodes, they will return from the function without doing anything.
2. Pre-Order Traversal#
Pre-Order traversal reads the nodes in a tree in a level-by-level order, left-child before right-child. The elements are read in a “root-left-right” order.
preOrderPrint(currentNode) {//if the currentNode IS NOT EQUAL to nullif (currentNode!==null) {//print its valueconsole.log(currentNode.val);//make recursive call to the left subtreethis.preOrderPrint(currentNode.leftChild);//make recursive call to the right subtreethis.preOrderPrint(currentNode.rightChild);}//if the currentNode IS EQUAL to null, then//we simply return}
class Node {constructor(value) {this.val = value;this.leftChild = null;this.rightChild = null;}}class BinarySearchTree {constructor(rootValue) {this.root = new Node(rootValue);}insert(currentNode, newValue) {if (currentNode === null) {currentNode = new Node(newValue);} else if (newValue < currentNode.val) {currentNode.leftChild = this.insert(currentNode.leftChild, newValue);} else {currentNode.rightChild = this.insert(currentNode.rightChild, newValue);}return currentNode;}insertBST(newValue) {if(this.root==null){this.root=new Node(newValue);return;}this.insert(this.root, newValue);}preOrderPrint(currentNode) {if (currentNode!==null) {console.log(currentNode.val);this.preOrderPrint(currentNode.leftChild);this.preOrderPrint(currentNode.rightChild);}}}var BST = new BinarySearchTree(6);console.log("The root val for BST : ", BST.root.val)BST.insertBST(4);BST.insertBST(9);BST.insertBST(5);BST.insertBST(2);BST.insertBST(8);BST.insertBST(12);BST.insertBST(10);BST.insertBST(14);BST.preOrderPrint(BST.root);
The algorithm for pre-order traversal, starting from the root node, is as follows:
- Visit the
currentNodeand display the data - Traverse the left subtree of
currentNoderecursively - Traverse the right subtree of
currentNoderecursively
Now let’s review the code for pre-order traversal.
We create a new object of the BinarySearchTree class and insert values into it. We then pass the root node to the preOrderPrint() function.
This function prints the value of the node, then it is recursively invoked for the left child. When the nodes in the left sub-tree have been visited, it is recursively invoked for the right child and its sub-trees.
When the recursive calls reach the null nodes, they will return from the function without doing anything.
3. Post-Order Traversal#
The last strategy for traversing a tree is the Post-Order traversal. Here, we traverse the left sub-tree, then the right subtree before we visit the root node. It takes a “left-right-root” order.
postOrderPrint(currentNode) {//if the currentNode IS NOT EQUAL to nullif (currentNode!==null) {//make recursive call to the left subtreethis.postOrderPrint(currentNode.leftChild);//make recursive call to the right subtreethis.postOrderPrint(currentNode.rightChild);//print its valueconsole.log(currentNode.val);}}
class Node {constructor(value) {this.val = value;this.leftChild = null;this.rightChild = null;}}class BinarySearchTree {constructor(rootValue) {this.root = new Node(rootValue);}insert(currentNode, newValue) {if (currentNode === null) {currentNode = new Node(newValue);} else if (newValue < currentNode.val) {currentNode.leftChild = this.insert(currentNode.leftChild, newValue);} else {currentNode.rightChild = this.insert(currentNode.rightChild, newValue);}return currentNode;}insertBST(newValue) {if(this.root==null){this.root=new Node(newValue);return;}this.insert(this.root, newValue);}preOrderPrint(currentNode) {if (currentNode !== null) {console.log(currentNode.val);this.preOrderPrint(currentNode.leftChild);this.preOrderPrint(currentNode.rightChild);}}inOrderPrint(currentNode) {if (currentNode !== null) {this.inOrderPrint(currentNode.leftChild);console.log(currentNode.val);this.inOrderPrint(currentNode.rightChild);}}postOrderPrint(currentNode) {if (currentNode !== null) {this.postOrderPrint(currentNode.leftChild);this.postOrderPrint(currentNode.rightChild);console.log(currentNode.val);}}}var BST = new BinarySearchTree(6);console.log("The root val for BST : ", BST.root.val)BST.insertBST(4);BST.insertBST(9);BST.insertBST(5);BST.insertBST(2);BST.insertBST(8);BST.insertBST(12);BST.postOrderPrint(BST.root);
The steps involved for post-order traversal are as follows:
- Traverse the left subtree of
currentNoderecursively - Traverse the right subtree of
currentNoderecursively - Visit the
currentNodeand print its value
Again, we create an object named BST and insert values into it. We will then pass the root node to the postOrderPrint() function as a starting point to the traversal.
If the node passed into the function is not null, this function calls postOrderPrint() on the left child first and then on the right child. Lastly, it prints the value of the currentNode.
The value of a parent node or the root node will only be printed once all the calls have been executed.
Level-Order (Breadth-First) Traversal#
With level-order traversal, trees are traversed level-wise. This means that we visit every node on a level from left to right before going to a lower level. All child nodes are traversed before the next level of grandchildren nodes.
This is similar to breadth-first search from graph algorithms.
traverseBFS() {if (!this.root) return;this.queue = [];this.queue.push(this.root);this.output = [];while (this.queue.length) {const node = this.queue.shift();if (node.left) {this.queue.push(node.left);}if (node.right) {this.queue.push(node.right);}this.output.push(node.data);}return this.output;}
In level-order traversal, we utilize a queue to store a reference to the node(s) we want to visit. This ensures that we can traverse the tree left-to-right on the same level.
When traversing the tree above, the root node would be the first to be placed in a queue, then the node with the value 12, then 18, 14, 16 and 20. The output would be:
[10,12,18,14,16,20]
Common interview questions#
That concludes what we need to know about tree traversal algorithms. The following are common coding interview questions about tree traversals that you should study:
- Find Nodes at “k” Distance from the Root.
- Check if given Preorder, In-order and Post order traversals are of the same tree.
- Print postorder traversals from given Preorder traversals.
- Implement Pre-order traversal without using recursion
- Can you do iterative Preorder traversal of a binary tree without recursion?
- What are advantages and disadvantages of BST?
You can continue learning about algorithms in JavaScript by visiting Educative’s learning path Ace the JavaScript Coding Interview. JavaScript continues to This path will take you through all that you need to know to crack your JavaScript interviews with confidence.
Happy learning!
Continue learning about JavaScript and algorithms#
Free Resources
