Tree traversal algorithms in Python every dev should know

Home/

Blog/

Programming/

11 mins read

Aug 28, 2022

Content

What are trees?

Tree nomenclature

How to traverse trees

Extending patterns to n-ary trees

Get hands-on with Ace the Python Coding Interview today.

Depth-first search

In-order traversal

Pre-order traversal

Post-order traversal

Level-order traversal (breadth-first) in Python

Python sketch (iterative)

Iterative templates vs recursion (and when to prefer each)

Iterative in-order uses a stack to walk left, visit, then right

Iterative pre-order

Iterative post-order

Choosing the right traversal: A quick guide

Breadth-first search algorithms

Complexity cheat sheet and gotchas

Common pitfalls

Master Python tree traversal algorithms today

Interview tips for essential tree traversal algorithms

Continue learning about Python, data structures, and algorithms

Algorithms are a significant part of a software engineer career, both in interviews and on the job. Many startups and FAANG companies like Facebook and Google focus majorly on algorithms and data structures during interviews, so understanding these concepts can be essential to advancing your career.

In addition, tech companies focus on designing the best algorithms to reduce server loading time, computational power, and so on, saving them a lot of time and resources. Therefore, it is important to understand how algorithms work and how they can be applied to specific computational tasks.

Today, we will discuss tree traversal algorithms in Python, which are commonly asked about during software engineering interviews.

We will specifically focus on Python over other programming languages due to its rising popularity among companies and easy-to-use syntax.

What are trees?#

In computer science terminology, trees are nonlinear hierarchical data structures.

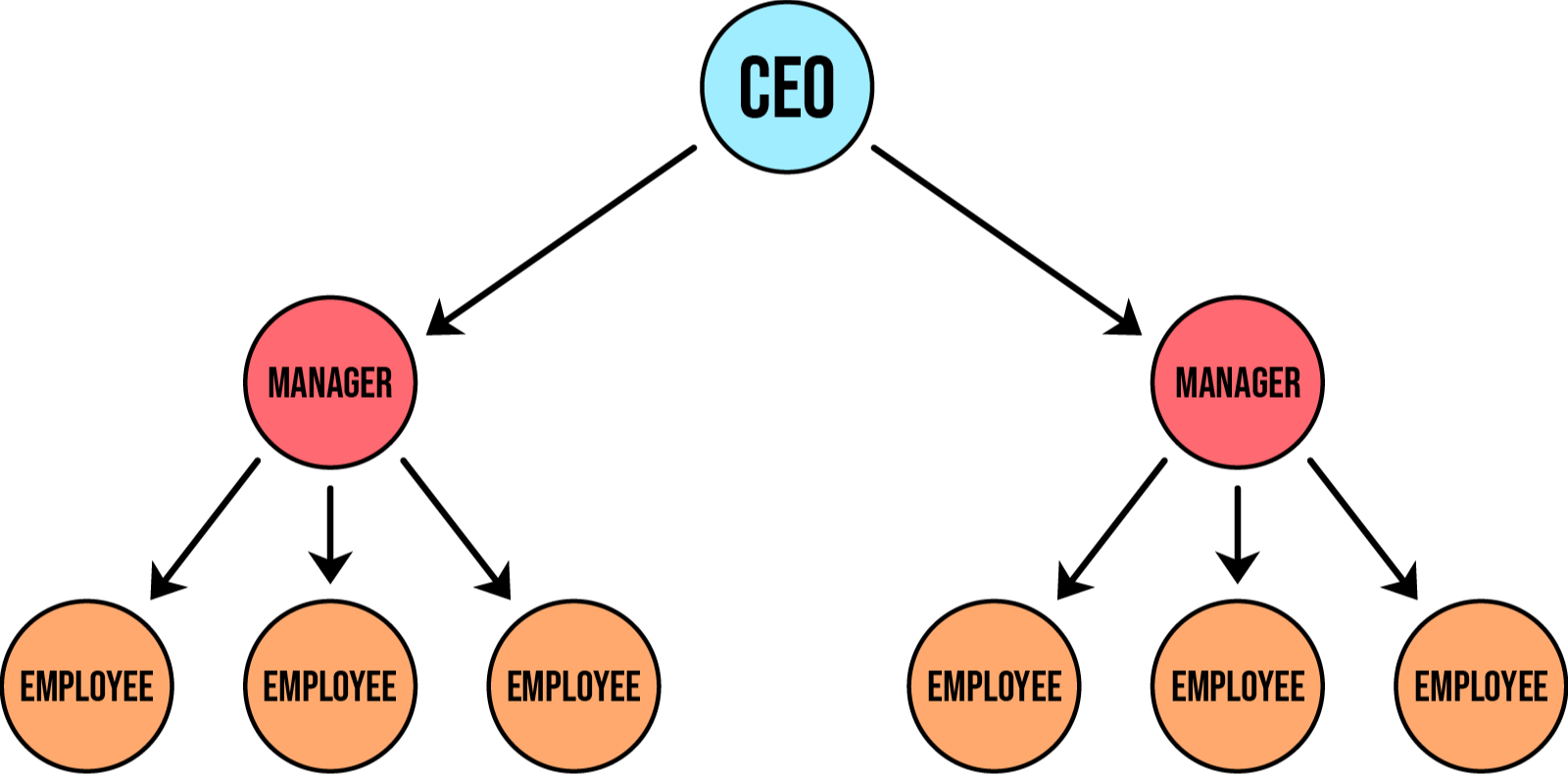
A tree contains a collection of nodes (also called vertices) where a pair of nodes are connected to each other with an edge. Unlike a graph a tree has no cycles (so it’s called acyclic). We can see a tree in action using a hierarchical company structure below:

Tree nomenclature#

Node: A node, or vertex, is a structure that may contain data and connections to other nodes (known as its children). A link between two nodes is referred to as an edge. An edge could be outgoing or incoming to a node. For instance, in the figure above Node-2 has an incoming edge from Node-1 and two outgoing edges to Node-4 and Node-5. Leaf node: A node with no outgoing edges is referred to as a leaf node. In the above example, Node-4, Node-8, Node-10, and Node-7 are leaf nodes.
Root node: A root node has no incoming edges to it. Typically it is considered the topmost node of the tree. In our example, Node-1 is the root node. Typically, a tree must have precisely a single root node.
Height of a node: The maximum number of edges from the node to a leaf node. In the above example, the heights of Node-3 and Node-4 are 3 and 0, respectively.
Depth of a node: The number of edges from the root to nodes in a tree. In the above example, the depth of Node-3 and Node-10 are 1 and 4, respectively.
Height of a tree: The height of the root node or depth of the deepest node.
Out-degree and in-degree of a node: A node’s in-degree refers to the number of edges coming in, whereas out-degree refers to the number of outgoing edges. In the above example, Node-3 has the in-degree of 1 but the out-degree of 2.
Pre-fix: This is where we access a tree starting from the root node first followed by the left child and then finally the right child.
Post-fix: This is where we access a tree starting from the left child first, then right child, and finally the root node.
In-fix: This is where we access a tree starting from the left child, the root node, and then finally the right child.

How to traverse trees#

Tree traversal is a process where we visit each and every node of a tree, optionally printing out data from those nodes. We always begin our search from the root node because all nodes are reachable from there.

There are two ways to traverse a tree. One is using the depth-first approach, and the second is using the breadth-first method.

Extending patterns to n-ary trees#

Most essential tree traversal algorithms transfer directly to n-ary trees with minimal changes:

DFS: recurse over each child in order (or push children to a stack in reverse order for iterative pre-order).
BFS: enqueue all children for each node you dequeue; level-size loops still segment levels cleanly.

The same templates handle generic XML/JSON-like hierarchies, org charts, or file systems. Start with the binary pattern, swap .left/.right for iterating .children, and retain the same queue/stack mechanics.

In-order traversal#

In this tree traversal method, we first visit the left sub-tree, then the root, and finally the right sub-tree.

Let’s look at in-order traversal in action. In the Python example below, we do the following:

Line 5-9: Create a Node class. The class has three members
- Left child: contains the left child of the node
- Right child: holds the right child of the node
- Data: the value of the node
Line 12-29: A function to insert data into the tree
Line 31-43: A function to print the tree
Line 46-54: Implementation of in-order traversal algorithm
Line 56-65: Insert several nodes in the tree and print the result of an in-order traversal

Python 3.8

from queue import Queue
 
queue = Queue()
class Node:
   def __init__(self, val):
 
       self.leftChild = None
       self.rightChild = None
       self.data = val
 
 
# Insert Node
   def insert(self, data):
       if data is None:
           return
       if self.leftChild is None:
           self.leftChild = Node(data)
           #print(self.data, '-- Left -->', data)
           data = None
       elif self.rightChild is None:     
           self.rightChild = Node(data)
           #print(self.data, '-- Right -->', data)
           data = None
       else:
           queue.put(self.leftChild)
           queue.put(self.rightChild)
 
       while queue.empty() is False:
           queue.get().insert(data)
 
# Print tree
   def printTree(self):
       ret = []
       ret.append(self.data)
       if self.leftChild is not None:
           queue.put(self.leftChild)
       if self.rightChild is not None:
           queue.put(self.rightChild)
 
       #print (len(stack))
       while queue.empty() is False:
           ret = ret + queue.get().printTree() 
       return ret
 
 
# Inorder traversal
# leftChild -> parent -> rightChild
   def inorderTraversal(self, root):
       ret = []
       if root:
           ret = self.inorderTraversal(root.leftChild)
           ret.append(root.data)
           ret = ret + self.inorderTraversal(root.rightChild)
       return ret
 
root = Node(27)
root.insert(14)
root.insert(5)
root.insert(10)
root.insert(6)
root.insert(31)
root.insert(9)
print("\n\nData is tree is = ", root.printTree())
 
print("\n\nresult of inorder traversal is = ", root.inorderTraversal(root))

Pre-order traversal#

When working with pre-order traversal, we visit the root node first, then the left sub-tree, and finally the right sub-tree.

In our example below, we will take the following steps:

Line 4-9: Create a Node class. The class has three members
- Left child: contains the left child of the node
- Right child: contains the right child of the node
- Data: the value of the node
Line 13-29: A function to insert data into the tree
Line 32-43: A function to print tree
Line 48-54: Implementation of pre-order traversal algorithm
Line 56-65: Insert several nodes in the tree and print the result of the pre-order traversal

Python 3.8

from queue import Queue
 
queue = Queue()
class Node:
   def __init__(self, val):
 
       self.leftChild = None
       self.rightChild = None
       self.data = val
 
 
# Insert Node
   def insert(self, data):
       if data is None:
           return
       if self.leftChild is None:
           self.leftChild = Node(data)
           #print(self.data, '-- Left -->', data)
           data = None
       elif self.rightChild is None:     
           self.rightChild = Node(data)
           #print(self.data, '-- Right -->', data)
           data = None
       else:
           queue.put(self.leftChild)
           queue.put(self.rightChild)
 
       while queue.empty() is False:
           queue.get().insert(data)
 
# Print tree
   def printTree(self):
       ret = []
       ret.append(self.data)
       if self.leftChild is not None:
           queue.put(self.leftChild)
       if self.rightChild is not None:
           queue.put(self.rightChild)
 
       #print (len(stack))
       while queue.empty() is False:
           ret = ret + queue.get().printTree() 
       return ret
 
 
# preorder traversal
# parent -> leftChild -> rightChild
   def preorderTraversal(self, root):
       ret = []
       if root:
           ret.append(root.data)
           ret = ret + self.preorderTraversal(root.leftChild)
           ret = ret + self.preorderTraversal(root.rightChild)
       return ret
 
root = Node(27)
root.insert(14)
root.insert(5)
root.insert(10)
root.insert(6)
root.insert(31)
root.insert(9)
print("\n\nData is tree is = ", root.printTree())
 
print("\n\nresult of preorder traversal is = ", root.preorderTraversal(root))

Post-order traversal#

As the name suggests, the post-order tree traversal is where we visit the root node last. In this traversal method, we traverse the left sub-tree first, followed by the right sub-tree, and finally the root.

Let’s learn by example. In the Python program below, we do the following:

Line 4-9: Create a Node class. The class has three members
- Left child: contains the left child of the node
- Right child: contains the right child of the node
- Data: the value of the node
Line 13-29: A function to insert data into the tree
Line 31-43: A function to print tree
Line 48-54: Implementation of post-order traversal algorithm
Line 56-65: Insert several nodes in the tree and print the result of the post-order traversal

Level-order traversal (breadth-first) in Python#

Level-order visits nodes one level at a time from the root down, which makes it ideal when you need the shallowest solution first, need by-level aggregates (e.g., max per level), or want to produce a breadth-wise serialization.

Implement it with a queue: enqueue the root, then repeatedly dequeue a node, process it, and enqueue its non-null children.
This is one of the essential tree traversal algorithms because it exposes structure by depth and naturally supports “zig-zag” or “level sums” variations with minimal changes.

Python sketch (iterative)#

from collections import deque

def level_order(root):
    if not root: 
        return []
    q, result = deque([root]), []
    while q:
        level_vals = []
        for _ in range(len(q)):
            node = q.popleft()
            level_vals.append(node.val)
            if node.left:  q.append(node.left)
            if node.right: q.append(node.right)
        result.append(level_vals)
    return result

Level-order is also a natural fit when transforming a tree into arrays of levels (for UI/tree maps) or when you need the shortest number of edges from the root to a qualifying node.

Iterative templates vs recursion (and when to prefer each)#

Python’s recursion is elegant for teaching essential tree traversal algorithms, but iterative patterns are interview-friendly and avoid recursion-depth limits.
The idea: replace the call stack with your own data structure.

Iterative in-order uses a stack to walk left, visit, then right#

def inorder_iter(root):
    stack, cur, output = [], root, []
    while cur or stack:
        while cur:
            stack.append(cur)
            cur = cur.left
        cur = stack.pop()
        output.append(cur.val)
        cur = cur.right
    return output

Iterative pre-order#

Push right then left (so left is processed first).

Iterative post-order#

Can use two stacks, or one stack plus a “last visited” pointer.

Prefer recursion for clarity and quick prototyping;
prefer iteration when the tree can be tall, when you must control space usage, or when the interviewer requests it.

For space-constrained in-order on binary trees, consider Morris traversal, which temporarily threads the tree to achieve O(1) extra space (but it mutates pointers during traversal and is less beginner-friendly).

Python 3.8

from queue import Queue
 
queue = Queue()
class Node:
   def __init__(self, val):
 
       self.leftChild = None
       self.rightChild = None
       self.data = val
 
 
# Insert Node
   def insert(self, data):
       if data is None:
           return
       if self.leftChild is None:
           self.leftChild = Node(data)
           #print(self.data, '-- Left -->', data)
           data = None
       elif self.rightChild is None:     
           self.rightChild = Node(data)
           #print(self.data, '-- Right -->', data)
           data = None
       else:
           queue.put(self.leftChild)
           queue.put(self.rightChild)
 
       while queue.empty() is False:
           queue.get().insert(data)
 
# Print tree
   def printTree(self):
       ret = []
       ret.append(self.data)
       if self.leftChild is not None:
           queue.put(self.leftChild)
       if self.rightChild is not None:
           queue.put(self.rightChild)
 
       #print (len(stack))
       while queue.empty() is False:
           ret = ret + queue.get().printTree() 
       return ret
 
 
# postorder traversal
# leftChild -> rightChild -> parent
   def postorderTraversal(self, root):
       ret = []
       if root:
           ret = ret + self.postorderTraversal(root.leftChild)
           ret = ret + self.postorderTraversal(root.rightChild)
           ret.append(root.data)
       return ret
 
root = Node(27)
root.insert(14)
root.insert(5)
root.insert(10)
root.insert(6)
root.insert(31)
root.insert(9)
print("\n\nData is tree is = ", root.printTree())
 
print("\n\nresult of postorder traversal is = ", root.postorderTraversal(root))

Choosing the right traversal: A quick guide#

In-order (binary search tree): yields sorted order of keys, perfect for exporting an ordered list or validating BST properties.
Pre-order: great for cloning/serializing structure top-down, building prefix expressions, or quickly capturing root-to-leaf paths.
Post-order: ideal when children must be processed before parents (e.g., freeing nodes, evaluating expression trees, computing subtree metrics).
Level-order: best for by-level analytics (width, averages), earliest-solution discovery by depth, and format outputs that mirror visual tree layers.

A practical rule: if the problem asks for “by level,” use level-order; if it asks for “children before parent,” use post-order; if it’s BST and needs sorted output, use in-order; for root-first tasks (copy, serialize), use pre-order. Also remember that in-order alone can’t uniquely serialize an arbitrary binary tree; pair it with pre- or post-order when structure must be preserved.

Breadth-first search algorithms#

Breadth-first search algorithms are commonly used on both trees and graphs. They’re implemented using recursion via data structures like lists and dictionaries.

The algorithms for breadth-first search (BFS) are as follows:

Pick any node in the tree or graph. Enqueue all adjacent nodes into a queue. Dequeue a vertex, and mark it as visited. Enqueue all adjacent nodes into another queue.
Repeat step 1 until all nodes have been visited or until you have arrived at your solution.
Be sure to mark all nodes you go through as visited before proceeding to the next ones to avoid being stuck in an infinite loop.

In our interactive code editor above in the depth-first traversal codes, our function printTree is printing tree using BFS. We encourage you to carefully observe our implementation of printTree and play around with it.

Complexity cheat sheet and gotchas#

Time complexity: All fundamental traversals (in-order, pre-order, post-order, level-order) visit each node once → O(n).
Space complexity:
- Recursion uses O(h) call stack (h = height).
- Iterative DFS uses O(h) stack; BFS uses O(w) queue (w = max nodes in a level).
- Morris in-order uses O(1) extra space but is specialized for binary trees and temporarily rewires pointers.

Common pitfalls#

Forgetting to mark/track visitation when adapting patterns to graphs (trees don’t need visited sets, graphs do).
Confusing DFS orders: “root-left-right” vs “left-root-right” vs “left-right-root.”

Assuming in-order gives sorted output on any tree—it does so only on a valid BST.

Master Python tree traversal algorithms today#

Congratulations on completing your journey into Python tree traversal algorithms! But we’ve just touched the surface of what you can do with tree traversal algorithms, which also includes practicing for interviews.

Several algorithmic interview questions will require you to solve problems using a tree data structure. Some common interview questions are:

Given a binary tree,
find its height
Binary tree in-order traversal
Maximum depth of a binary tree
Sum root to leaf numbers

Interview tips for essential tree traversal algorithms#

Memorize two templates: iterative in-order and level-order. You can derive pre-/post-order from the in-order template by rearranging when you “visit.”
Narrate choices: explain why you picked DFS vs BFS for the asked output shape.
Edge cases: empty tree, single node, skewed tree (test recursion depth), and unbalanced width (test BFS memory).
Output shape: decide early whether you need a flat list, per-level lists, or a string serialization; this dictates traversal order.

Written By:

Sadia Suhail

Free Resources

blog

What are REST APIs? HTTP API vs. REST API

blog

How does prompt engineering differ from traditional programming?

blog

10 common mistakes Python programmers make (and how to fix them)

Tree traversal algorithms in Python every dev should know

What are trees?#

Tree nomenclature#

How to traverse trees#

Extending patterns to n-ary trees#

Get hands-on with Ace the Python Coding Interview today.#

Depth-first search#

In-order traversal#

Pre-order traversal#

Post-order traversal#

Level-order traversal (breadth-first) in Python#

Python sketch (iterative)#

Iterative templates vs recursion (and when to prefer each)#

Iterative in-order uses a stack to walk left, visit, then right#

Iterative pre-order#

Iterative post-order#

Choosing the right traversal: A quick guide#

Breadth-first search algorithms#

Complexity cheat sheet and gotchas#

Common pitfalls#

Master Python tree traversal algorithms today#

Interview tips for essential tree traversal algorithms#

Continue learning about Python, data structures, and algorithms#