Computer Number Systems 101: Binary & Hexadecimal Conversions
When we type words onto a computer, it will translate them into numbers. In fact, to a computer, all information is written as series of 1s and 0s. Computer number systems are how we represent numbers in a computer system architecture.
Number systems are one of the most fundamental concepts that computer scientists must learn. It’s an important step for anyone who wants to become a computer scientist or programmer.
Today, we will introduce you to the number systems that are essential for a computer scientist. We’ll take a deep dive into the binary and hexadecimal number systems.
Learn to code today.#
Try one of our courses on programming fundamentals:
What is a number system in computer science?#
Humans have been counting for a long time. To do so, we use systems that relate unique symbols to specific values. This is called a number system, and it is the technique that we use to represent and manipulate numbers
A number system must have unique symbols for every value, be consistent, provide comparable values, and be easily reproducible.
You are probably most familiar with the decimal system that forms the basis of how humans count. The decimal system has a base of 10, because it provides 10 symbols to represent all numbers:
Humans use the decimal system because we have 10 fingers to count on, but machines don’t have that luxury. So, we’ve created other number systems that perform the same functions. Computers represent information differently than humans, so we need different systems to represent numbers.
Computers support the following number systems:
- Binary
- Octal
- Decimal
- Hexadecimal
Introduction to the Binary Number System#
A computer uses bits to represent information. A bit is the most basic unit of storage in a computer. An essential component of computers is called the transistor. Just like a light switch, the transistor either allows or prevents current to flow. So, it only has two states: on and off.
Every number in a computer is an electrical signal. In the early days of computers, electrical signals were representing with an “on” state (a negative charge) and an “off” state (a positive charge). This forms a kind of binary switch.
These two states can be represented using one of two symbols: 1 and 0. This means that the binary number system has a base of 2. Only symbols are needed to represent every number.
The base digits for the binary system are simple: 0 to represent a low state, and 1 to represent a high state.
Instead of representing numbers as individual units (like the number 10 or 400), we use groups of 1s and 0s. For example, here is what it looks like when a computer counts from 0 to 10:
This is called the binary number system. Each binary digit is referred to as a bit. For instance, is composed of 4-bits which are , , , and . When it comes to placing values to the bits (i.e. digits) in this system, we place values corresponding to ascending powers of 2 from right to left.
The rightmost bit is called the least significant bit (LSB), and the leftmost bit is the most significant bit (MSB).
You can manipulate bits left and right with bitwise operators to efficiently change the value of a number at the machine code level.
Convert between Decimal and Binary#
Now that we know the basics of the binary system, let’s learn how we’d convert between decimal and binary. We begin with binary to decimal conversion.
We know that the binary system has place values of powers of 2. These values are weights for the digits (0 or 1) in those positions. Here’s how it works:
- We multiply each digit by its weight (its position multiplied by 2)
- We sum them all up to get the decimal number
So, let’s take the binary number 11111010 and convert it to the decimal number system.
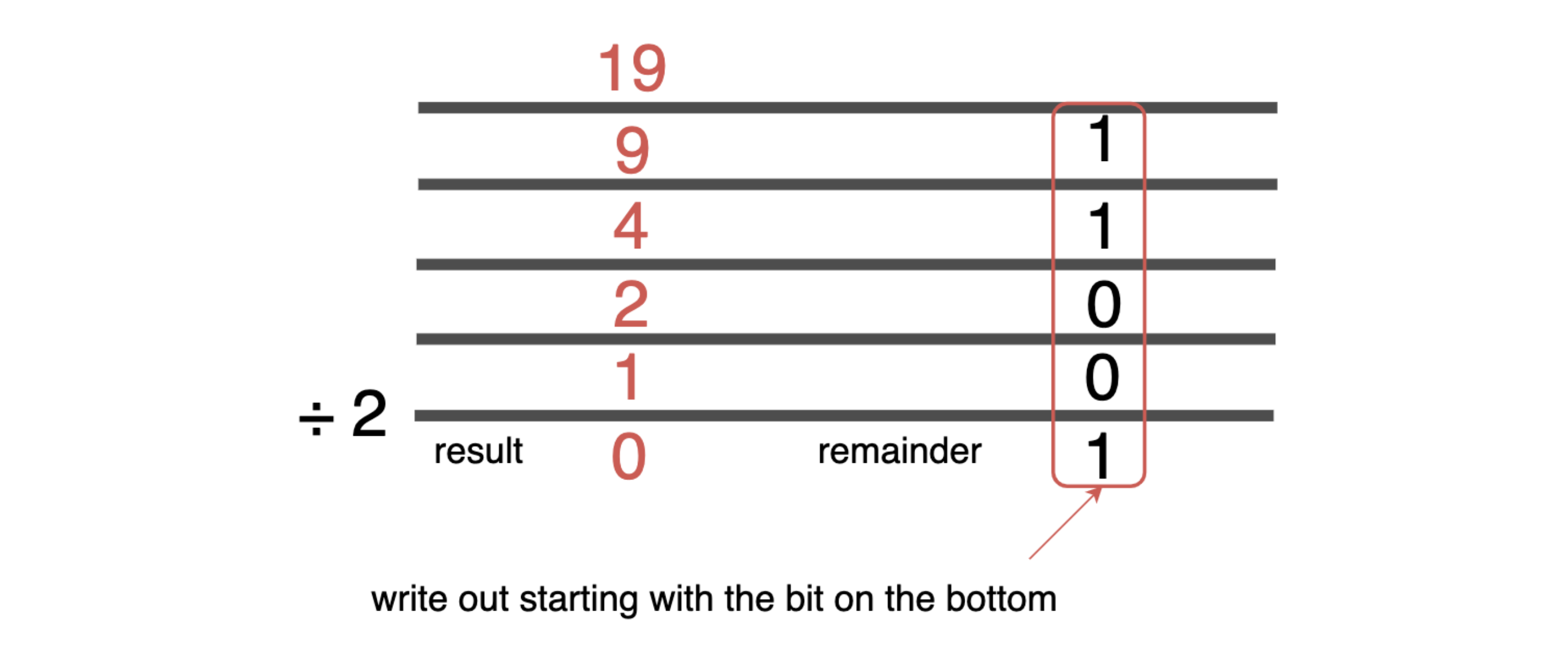
Now let’s try it the other way around. How do we convert from a decimal to a binary number? One method to do this is repeated division, which is a handy shortcut.
So, take the number 19. We start by dividing it by two and writing down the remainder. When we divide 19 by 2, we get 9 with a remainder of 1.
We then take 9 and divide it by 2, giving us a result of 4 with a remainder of 1. This process continues until we reach zero. The remainders that we gathered form our binary number!
Repeatedly dividing by 2 and keeping track of the remainders is a shortcut for converting decimal to binary!
Try it out yourself!
What is the binary representation of 94?
1001110
0111101
1011110
Introduction to the Hexadecimal Number System#
Now that we’ve learned a bit about the binary system, let’s learn about another common system used by computers: the hexadecimal number system.
Binary numbers are easy for computers but not so easy for humans to understand. And when you’re working with large numbers, it becomes difficult to both write without error. So, to fix this problem we can arrange binary numbers into groups of four bits, forming the hexadecimal number system.
The hexadecimal system is amore compact way of representing numbers on a computer, as it requires only 4 bits to represent a digit’s value.
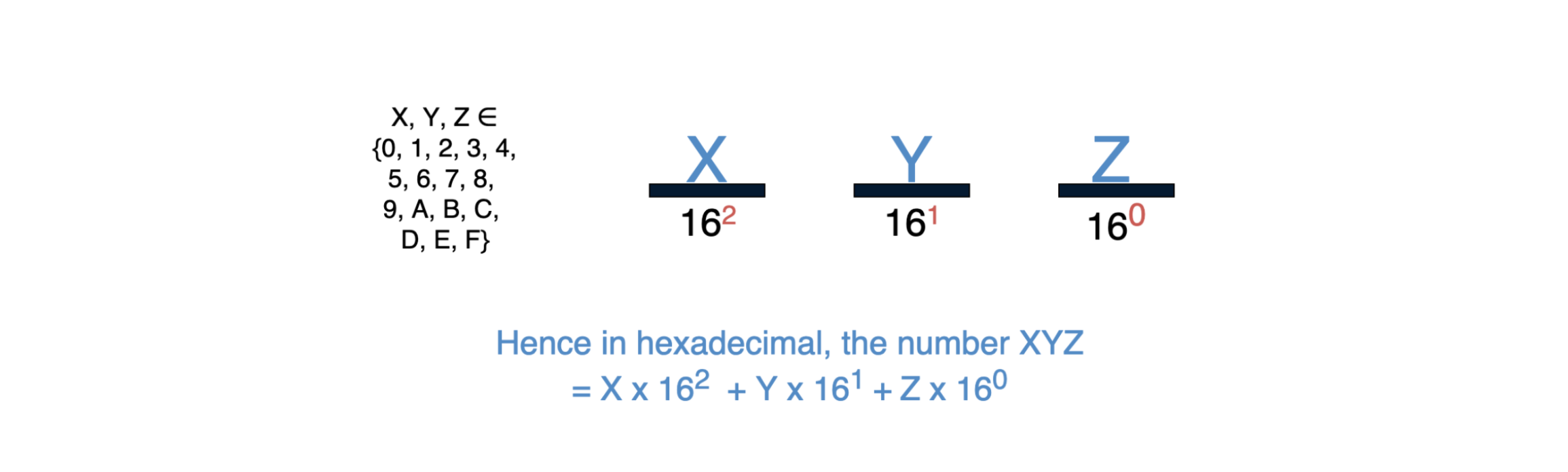
The hexadecimal system (often called “hex”) is made up of 16 symbols, so it has a base of 16. Hexadecimal uses the 10 numbers of the decimal system and six extra symbols, A, B, C, D, E and F.
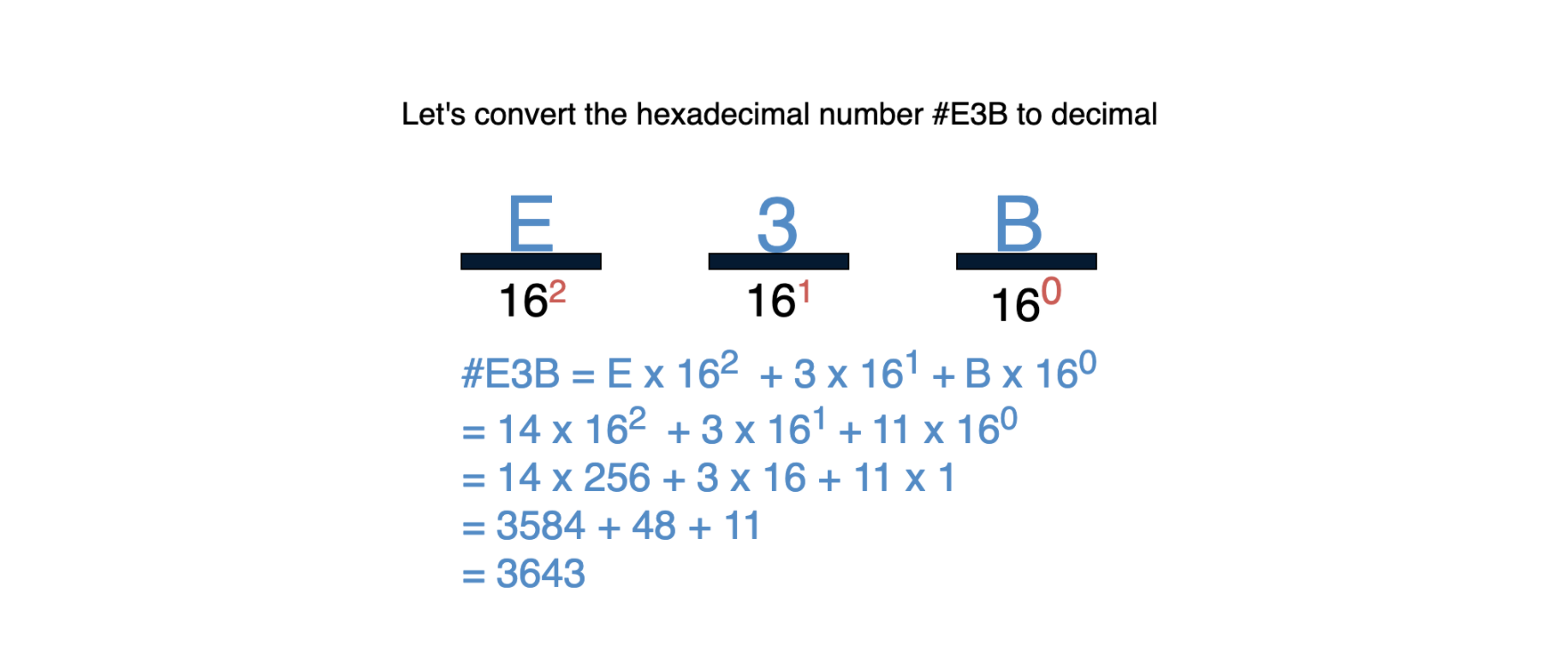
The place values in hexadecimal are powers of 16. Let’s see what the hexadecimal number XYZ would be in decimal. As you can see below, hexadecimal numbers are preceded by a # to indicate that they are base-16.
Learn to code today.#
Try one of our courses on programming fundamentals:
How to convert between binary and hexadecimal#
Now that we understand both the binary and the hexadecimal number systems, let’s learn about binary and hexadecimal conversions. We begin with binary to hexadecimal.
We will group the binary digits into sets of four (starting on the right). Then, we replace each quartet with the corresponding hexadecimal representation.
Now for hexadecimal to binary! Let’s go through an example. Below, we are expanding each hexadecimal digit by replacing it with its equivalent binary quartet.
What is the octal number system?#
The octal number system is not as widely used as hex of binary. It was developed under the same idea as the hexadecimal system: to make binary more compact.
The octal system groups binary numbers into triplets instead of quartets. So, the octal system is base-8, as .
We use eight base symbols for the octal system that are borrowed from the decimal system. Binary triplets can have values ranging from .
So, the place values will be ascending in powers of from right to left.
To convert binary to octal, we follow this basic technique:
- Group the binary number into sets of three (similar to what we did with hex)
- Bring each group of digits to a multiple of three by adding zeroes
- Write the corresponding octal symbol underneath each group
- You will now have an octal number
Converting octal to binary is similar but a bit simpler:
- Write the binary representation for each octal digit
- Join those numbers together
- You will not have a binary number
What to learn next#
Congrats! You now have a solid introduction to number systems for computer science. You’ve taken your first fundamental step into the world of computer programming.
Now that you know these basics, you can start mastering your first programming language with one of our courses:
- Learn to Code: Python for Absolute Beginners
- Learn to Code: C++ for Absolute Beginners
- Learn to Code: C# for Absolute Beginners
- Learn to Code: Java for Absolute Beginners
- Learn to Code: JavaScript for Absolute Beginners
- Learn to Code: Ruby for Absolute Beginners
Happy learning!
Continue reading about computer science#
Free Resources
